The math constant e can be computed using the following series (also see this, this and this post):
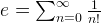
i.e. 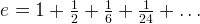
If we combine every two iterations, we will get something like,
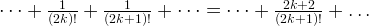
If we combine every three iterations, we will get something like,
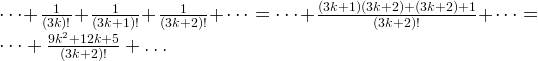 .
.
I guess, you can keep doing this and combine more iterations.
OK, so what is this going and what is the good doing this? Let’s write a Python script to compare how they converge to e = 2.71828182845904523536.
#!/usr/bin/env python
# https://helloacm.com
#fact = lambda x: x and x * fact(x - 1) or 1
def compute(n):
k1 = 1
k2 = 1
k3 = 2
s1 = 1.0
s2 = 2.0
s3 = 2.5
for i in xrange(1, n + 1):
k1 *= i
s1 += 1.0 / k1
k2 *= (2 * i) * (2 * i + 1)
s2 += (2 * i + 2.0) / k2
k3 *= (3 * i) * (3 * i + 1) * (3 * i + 2)
s3 += (9 * (i**2) + 12 * i + 5.0) / k3
print i, chr(9), s1, chr(9), s2, chr(9), s3
if __name__ == "__main__":
compute(25)
The above script computes the convergence value each step using the original series, 2-step combined and 3-step combined. It produces the following, as expected.
1 2.0 2.66666666667 2.71666666667 2 2.5 2.71666666667 2.71827876984 3 2.66666666667 2.71825396825 2.7182818262 4 2.70833333333 2.71828152557 2.71828182846 5 2.71666666667 2.7182818262 2.71828182846 6 2.71805555556 2.71828182845 2.71828182846 7 2.71825396825 2.71828182846 2.71828182846 8 2.71827876984 2.71828182846 2.71828182846 9 2.71828152557 2.71828182846 2.71828182846 10 2.71828180115 2.71828182846 2.71828182846 11 2.7182818262 2.71828182846 2.71828182846 12 2.71828182829 2.71828182846 2.71828182846 13 2.71828182845 2.71828182846 2.71828182846 14 2.71828182846 2.71828182846 2.71828182846 15 2.71828182846 2.71828182846 2.71828182846 16 2.71828182846 2.71828182846 2.71828182846 17 2.71828182846 2.71828182846 2.71828182846 18 2.71828182846 2.71828182846 2.71828182846 19 2.71828182846 2.71828182846 2.71828182846 20 2.71828182846 2.71828182846 2.71828182846 21 2.71828182846 2.71828182846 2.71828182846 22 2.71828182846 2.71828182846 2.71828182846 23 2.71828182846 2.71828182846 2.71828182846 24 2.71828182846 2.71828182846 2.71828182846 25 2.71828182846 2.71828182846 2.71828182846
In simple words, the second series is about twice as fast as the first one, and the third is about three times faster in obtaining the value of e. e.g, the native version (first approach) reaches the value at iteration 14 while the second method arrives the same value at iteration 7.
No surprise, the speed (in this case, we are referring to the number of iterations, not the total amount of operations, which are on similar scales), is proportional. However, the 1/n! vanishes to machine-precision much faster, than e.g., 2n/n!, which is the more important point of combining (compressing) the series.
–EOF (The Ultimate Computing & Technology Blog) —
loading...
Last Post: Parse a Filename using Scripting.FileSystemObject
Next Post: Stackoverflow: Why doesn't the optimizer eliminate High in a loop?