A Better SteemIt Voting Strategy with Back Tracking Algorithm

In last post, three voting strategies were presented. But we are not sure if there are better ones. Let’s review this:

• vote all once you wake up
• vote all once before you go to bed
• vote and rest at a specific time interval

By using Javascript simulations, we happen to know that if the P is closer to 100%, we choose the ‘vote and rest’ strategy, otherwise, we can just vote all once right before the timespan ends.

This post, we use the backtracking to search all possible strategy solutions. The search space is huge and that is why we make T and N smaller i.e. N=4 (4 hours) and T=4 (4 upvotes per day). M=270 which is 100% payout in unit of dollars.

Let’s create an array that contains the minutes offsets (from the start) for each votes.

1
2
3
4

var sol = Array();
for (var i = 0; i < T; ++ i) {
    sol[i] = 0;
}

var sol = Array();
for (var i = 0; i < T; ++ i) {
    sol[i] = 0;
}

For example,

1

sol = [1, 2, 3, 4, 5, 6, 7, 8];

sol = [1, 2, 3, 4, 5, 6, 7, 8];

The sol represents voting every minute from the minute 1. There are 8 votes. We initialize the sol array to zeros meaning voting all once at the begining (with zero minute offset)

Let’s also declare two variables, one stores the solutions and the other stores the maximum payout.

1
2

var bestSol = sol.slice(0);
var bestScore = 0;

var bestSol = sol.slice(0);
var bestScore = 0;

We need to print out the solutions once we find the best one.

1
2
3
4
5
6
7

function print(sol) {
    var s = "";
    for (var i = 0; i < T; ++ i) {
        s += sol[i] + ", ";
    }
    console.log(s);
}

function print(sol) {
    var s = "";
    for (var i = 0; i < T; ++ i) {
        s += sol[i] + ", ";
    }
    console.log(s);
}

We need a evaluation function that computes the payout given a solution. Every minute, the SP restores 0.005/36.

1
2
3
4
5
6
7
8
9
10
11
12

function eval(sol, P, M, T, N) {
    var sp_restored = 0.005 / 36;
    P = Math.min(1, P + sp_restored * (sol[0])); // Max = 100% 
    var x = 0;
    sol[T] = sol[T - 1]; //  Avoid out of range access for sol[i+1]
    for (var i = 0; i < T; ++ i) {
        x += P * M;  // Accumulate Payout 
        P -= 0.02;    // 2% loss
        P += sp_restored * (sol[i + 1] - sol[i]); // SP restores before next vote 
    }
    return x;       
}

function eval(sol, P, M, T, N) {
    var sp_restored = 0.005 / 36;
    P = Math.min(1, P + sp_restored * (sol[0])); // Max = 100% 
    var x = 0;
    sol[T] = sol[T - 1]; //  Avoid out of range access for sol[i+1]
    for (var i = 0; i < T; ++ i) {
        x += P * M;  // Accumulate Payout 
        P -= 0.02;    // 2% loss
        P += sp_restored * (sol[i + 1] - sol[i]); // SP restores before next vote 
    }
    return x;       
}

The best part is: the search algorithm. We enforce a 15-minute interval between intermediate votes unless the votes come to the end. The reason for doing this is that the search space is really huge and you can’ t basically finish the search on standard PC. The backtracking can be seen as a search tree, where we start from the root, go as deep as we can, expand to the sibling nodes, and rewind to the parents.

We don’t have the cut-off techniques here, meaning that when we vote at time t, the next votes could happen at t, t+1, t+2 until the end of timespan. The branch factor for this search tree is 60N (assume that all votes are placed at the same time), the depth of the search tree is T, obviously.

The search space is around 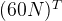and we certainly do not have time to bruteforce all possible solutions. With backtracking, the runtime complexity can be seen as 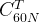i.e. the total number of different solutions to pick T from 60N.

The Javascript code for the backtracking search is:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

function search(sol, left, n, T, right) {
    if (n == T) { // when we reach the tree leaves
        var score = eval(sol, P, M, T, N);  // need to evaluate this solution 
        if (score > bestScore) {  // found a better solution?
                bestScore = score;
                bestSol = sol.slice(0);
            }
            return; 
    }
    for (var i = left; i <= right; ++ i) {
        sol[n] = i;  // The n-th vote is placed at time 
        search(sol, Math.min(right, i + 15), n + 1, T, right); // try next vote 
    }
}

function search(sol, left, n, T, right) {
    if (n == T) { // when we reach the tree leaves
        var score = eval(sol, P, M, T, N);  // need to evaluate this solution 
        if (score > bestScore) {  // found a better solution?
                bestScore = score;
                bestSol = sol.slice(0);
            }
            return; 
    }
    for (var i = left; i <= right; ++ i) {
        sol[n] = i;  // The n-th vote is placed at time 
        search(sol, Math.min(right, i + 15), n + 1, T, right); // try next vote 
    }
}

Windows + sublimit text3 + Node.js, we run and get these numbers:

When P=0.99

calcPayout0 =  1036.8
calcPayout1 =  1047.6
calcPayout2 =  1054.8
calcPayout3 =  1066.5
72, 240, 240, 240, 

The first vote should happen at minute 72 where the rest 3 should be at the end, which has earned 12 SBD more.

When P=0.8 (80%)

calcPayout0 =  831.5999999999999
calcPayout1 =  867.5999999999999
calcPayout2 =  849.5999999999999
calcPayout3 =  867.5999999999999
240, 240, 240, 240

Use all votes at the end is clearly the optimal.

When P=1 (100%)

calcPayout0 =  1047.6
calcPayout1 =  1047.6
calcPayout2 =  1065.6
calcPayout3 =  1074.6000000000001
0, 240, 240, 240, 

Use only 1 vote at the begining and the rest at the end.. This problem is NP-hard, where you just have to know that it is VERY HARD problem, in WIKI, it describes as follows:

NP-hardness (non-deterministic polynomial-time hardness), in computational complexity theory, is the defining property of a class of problems that are, informally, “at least as hard as the hardest problems in NP”. More precisely, a problem H is NP-hard when every problem L in NP can be reduced in polynomial time to H, that is: assuming a solution for H takes 1 unit time, we can use H‎’s solution to solve L in polynomial time.[1][2] As a consequence, finding a polynomial algorithm to solve any NP-hard problem would give polynomial algorithms for all the problems in NP, which is unlikely as many of them are considered hard.[3]

OK, so the preliminary conclusion is: when P is closer to 100%, you might want to try place your first vote at the begining, and the rest right at the end. However, there might be better solutions, i.e. we enforce a 15-minute voting interval here.

You may also like: SteemIt 通过回溯算法确定更好的点赞策略 （高级版）

–EOF (The Ultimate Computing & Technology Blog) —