How to Solve Matrix Chain Multiplication using Dynamic Programming?

The Matrix Chain Multiplication Problem is the classic example for Dynamic Programming. If there are three matrices: A, B and C. The total number of multiplication for (A*B)*C and A*(B*C) is likely to be different. For example, if the dimensions for three matrices are: 2×3, 3×5, 5×9 (please note that the two matrices can be multiplied if and only if the columns of first matrix is equal to the rows of the second matrix),

If we multiple matrices in this order (A*B)*C, the total number of multiplication equals to 2*3*5+2*5*9=120
If we multiple matrices in this order A*(B*C), the total number of multiplication equals to 3*5*9+2*3*9=189
Noted that if two matrices dimensions are a*b, b*c then the number of multiplication for these matrices are a*b*c.

Clearly, the first approach is better. But if there are n matrices, the total number of possibilities grow exponentially (ways to multiple matrices). Bruteforce clearly can’t solve this problem efficiently.

DP Equations

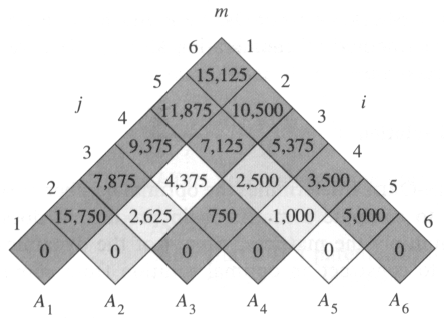
DP solves the problem where the optimal solution is also part of sub-problems. For example, if we know the best way is to divide the matrix chain at position n and make f(m, n) the answer to do multiplication between Matrix m and n inclusive, then the following holds:

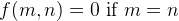
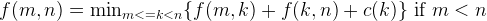
Recursion

The c(k) is the number of multiplication if you multiple matrix k and k+1. Therefore, the psudo code for the above equations can be written as:

1
2
3
4
5
6
7
8
9
10
11

int matrix_chain(int *matrix, int m, int n) {
  if (m == n) return 0;
  int ans = MAXINT;
  for (int i = m; i < n; i ++) {
    int cost = matrix_chain(matrix, m, i) + matrix_chain(matrix, i + 1, n) + matrix[i].rows * matrix[i].columns * matrix[i+1].columns;
    if (cost < ans) {
      ans < cost;
    }
  }
  return ans;
}

int matrix_chain(int *matrix, int m, int n) {
  if (m == n) return 0;
  int ans = MAXINT;
  for (int i = m; i < n; i ++) {
    int cost = matrix_chain(matrix, m, i) + matrix_chain(matrix, i + 1, n) + matrix[i].rows * matrix[i].columns * matrix[i+1].columns;
    if (cost < ans) {
      ans < cost;
    }
  }
  return ans;
}

Memorization

The above recursion is straightforward implementation but as many intermediate results are computed over and over again, this approach is still slow in practice. One easy method to improve this is to store the results in a look-up. This will prevent the repetitive calculations.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

// global lookup[][]
int matrix_chain(int *matrix, int m, int n) {
  if (m == n) {
    lookup[m, n] = 0;
    return 0;
  }
  if (lookup[m, n] != -1) return lookup[m, n];
  int ans = MAXINT;
  for (int i = m; i < n; i ++) {
    int cost = matrix_chain(matrix, m, i) + matrix_chain(matrix, i + 1, n) + matrix[i].rows * matrix[i].columns * matrix[i+1].columns;
    if (cost < ans) {
      ans < cost;
    }
  }
  lookup[m, n] = ans; // storing the answer
  return ans;
}

// global lookup[][]
int matrix_chain(int *matrix, int m, int n) {
  if (m == n) {
    lookup[m, n] = 0;
    return 0;
  }
  if (lookup[m, n] != -1) return lookup[m, n];
  int ans = MAXINT;
  for (int i = m; i < n; i ++) {
    int cost = matrix_chain(matrix, m, i) + matrix_chain(matrix, i + 1, n) + matrix[i].rows * matrix[i].columns * matrix[i+1].columns;
    if (cost < ans) {
      ans < cost;
    }
  }
  lookup[m, n] = ans; // storing the answer
  return ans;
}

Iterative

Almost every recursions (except some cases, such as Ackerman) can be rewritten into a more-efficient iterative approach. We would need to compute the DP tree from the leafs to the root. Therefore, we need to increment the chain length.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

int matrix_chain(int *matrix, int M, int N) {
    int n = matrix.length;
    m = new int[n][n];
    s = new int[n][n];
 
    for (int ii = 1; ii < n; ii++) { // chain length
        for (int i = 0; i < n - ii; i++) {
            int j = i + ii;
            m[i][j] = MAXINT;
            for (int k = i; k < j; k++) {
                int q = m[i][k] + m[k+1][j] + matrix[i]*matrix[k+1]*matrix[j+1];
                if (q < m[i][j]) {
                    m[i][j] = q;
                    s[i][j] = k;
                }
            }
        }
    }
    return m[M][N];
}

int matrix_chain(int *matrix, int M, int N) {
    int n = matrix.length;
    m = new int[n][n];
    s = new int[n][n];

    for (int ii = 1; ii < n; ii++) { // chain length
        for (int i = 0; i < n - ii; i++) {
            int j = i + ii;
            m[i][j] = MAXINT;
            for (int k = i; k < j; k++) {
                int q = m[i][k] + m[k+1][j] + matrix[i]*matrix[k+1]*matrix[j+1];
                if (q < m[i][j]) {
                    m[i][j] = q;
                    s[i][j] = k;
                }
            }
        }
    }
    return m[M][N];
}

chainMatrix-m-table

The above algorithms run at complexity O(n³).

--EOF (The Ultimate Computing & Technology Blog) --