N Queen Problem in Back Tracing, Bit-logics

github: https://github.com/DoctorLai/Algorithms/tree/master/Queen

n Queen problem can be dated back in 1848. Later, it was popular used in computer algorithm books that teach data structure and algorithms. The problem is to find the number of ways to put n queens in n x n size of chess board so that each queens do not attach each other (vertically, horizontally and diagonally).

For example, the following is a solution of 8 queen problem.

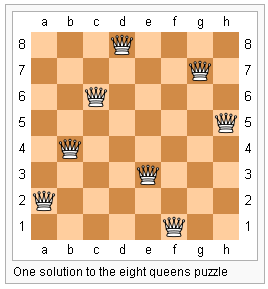
The algorithm to search for solution is to check one by one (row by row or column by column) and place each queen individually. The counter (answer) will be incremented by one if n queens are placed sucessfully.

If queens can be placed diagonally, the total solutions would be 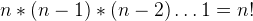. However, brute-force these solutions and check for diagonal attacks will be very time-consuming. Ideally, if on current row, there is an attacking situation, there will be no further need to check next solutions that are also attacking  because the current queen attacks or are being attached. This is call branch-cut-off, which saves a lot of time by avoiding unnecesary solution checks.

The following is recursive back tracing that tries to iterate each valid solution.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

#!/usr/bin/env python
# https://helloacm.com
 
from time import *
 
# size of queen
n = 10
 
# recursive back tracing
ans = 0
sol = [0] * n
 
def chk(sol, depth):
    if depth == 0:
        return True
    for i in xrange(0, depth):
        if sol[i] == sol[depth]:
            return False
        if abs(i - depth) == abs(sol[i] - sol[depth]):
            return False
    return True;
 
def work(depth, row):
    global sol, ans, n
    if depth == n:
        ans += 1
        return
    for i in xrange(0, n):
        sol[depth] = i
        if chk(sol, depth):
            work(depth + 1, 0)
 
start = time()
work(0, 0)
print time() - start
print ans

#!/usr/bin/env python
# https://helloacm.com

from time import *

# size of queen
n = 10

# recursive back tracing
ans = 0
sol = [0] * n

def chk(sol, depth):
    if depth == 0:
        return True
    for i in xrange(0, depth):
        if sol[i] == sol[depth]:
            return False
        if abs(i - depth) == abs(sol[i] - sol[depth]):
            return False
    return True;

def work(depth, row):
    global sol, ans, n
    if depth == n:
        ans += 1
        return
    for i in xrange(0, n):
        sol[depth] = i
        if chk(sol, depth):
            work(depth + 1, 0)

start = time()
work(0, 0)
print time() - start
print ans

The timing on 8GB, Intel Core7, Win7 is 0.628999948502 seconds for 10 queens.

The other quick implementation is based on bit-logic operations. It is extremely fast. The following is the approach.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

#!/usr/bin/env python
# https://helloacm.com
 
from time import *
 
# size of queen
n = 10
 
# bit hack version
ans = 0
LIM = (1 << n) - 1
 
def queen(row, ld, rd):
    # row: which queen
    # ld: left diag
    # rd: right diag
    global ans, LIM
    if row == LIM:
        ans += 1
        return
    pos = LIM & (~(row | ld | rd)) # valid positions
    while pos != 0:
        p = pos & (-pos)  # try rightmost one
        pos -= p;
        queen(row + p, (ld + p) << 1, (rd + p) >> 1) # recursive next queen
 
start = time()
queen(0, 0, 0)
print time() - start
print ans

#!/usr/bin/env python
# https://helloacm.com

from time import *

# size of queen
n = 10

# bit hack version
ans = 0
LIM = (1 << n) - 1

def queen(row, ld, rd):
    # row: which queen
    # ld: left diag
    # rd: right diag
    global ans, LIM
    if row == LIM:
        ans += 1
        return
    pos = LIM & (~(row | ld | rd)) # valid positions
    while pos != 0:
        p = pos & (-pos)  # try rightmost one
        pos -= p;
        queen(row + p, (ld + p) << 1, (rd + p) >> 1) # recursive next queen

start = time()
queen(0, 0, 0)
print time() - start
print ans

On the same problem-scale, same machine, it finds the solution within 0.024 seconds, which is a lot faster than the above approach.

The queen function takes three parameters, row, ld, rd representing the forbidden places of current row, left diagonal and right diagonal respectively.

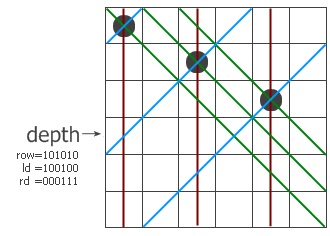
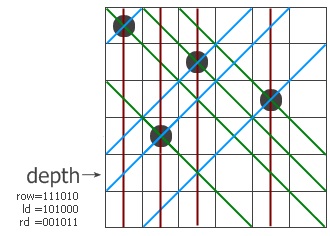
The row | ld | rd combines all invalid positions. ~ is the boolean not operation which gives the valid position. p & -pos equals to the right-most one. i.e. -pos = ~pos + 1

Then on next recursive call, we try the next queen by updating the forbidden places. When the row equals to all ones, we have a solution and increase the counter by one. Simple, powerful and effective!

Other classic implementations of backtracking algorithms to solve the N queen problem: Using Recursive Backtracking Algorithm to Solve Classic N Queen Problem

See other implementations of N-Queen Problems:

• Algorithm to Valid N Queens
• Teaching Kids Programming – Backtracking Algorithm to Solve N-Queen Problem
• Using Recursive Backtracking Algorithm to Solve Classic N Queen Problem
• Find the Queens That Can Attack the King
• N Queen Problem in Back Tracing, Bit-logics
• Coding Exercise – N Queen Problem – C++ – Bit Logics – Shortest and Fastest Solution – Online Judge
• N Queen Problem in Back Tracing, Bit-logics

–EOF (The Ultimate Computing & Technology Blog) —