Teaching Kids Programming – Compute the Number of Trailing Zeros for Factorial N

Teaching Kids Programming: Videos on Data Structures and Algorithms

Given an integer n, return the number of trailing zeroes in n! Could you write a solution that works in logarithmic time complexity?

Example 1:
Input: n = 3
Output: 0
Explanation: 3! = 6, no trailing zero.

Example 2:
Input: n = 5
Output: 1
Explanation: 5! = 120, one trailing zero.

Example 3:
Input: n = 0
Output: 0

Bruteforce Algorithm to Compute the Trailing Zeros for Factorial

First compute the actual factorial value, then count the number of zeros:

1
2
3
4
5
6
7
8
9
10
11

def trailingZeroes(n: int) -> int:
    # Calculate n!
    n_factorial = 1
    for i in range(2, n + 1):
        n_factorial *= i
    # Count how many 0's are on the end.
    zero_count = 0
    while n_factorial % 10 == 0:
        zero_count += 1
        n_factorial //= 10
    return zero_count

def trailingZeroes(n: int) -> int:
    # Calculate n!
    n_factorial = 1
    for i in range(2, n + 1):
        n_factorial *= i
    # Count how many 0's are on the end.
    zero_count = 0
    while n_factorial % 10 == 0:
        zero_count += 1
        n_factorial //= 10
    return zero_count

Time complexity O(N^2) as we can’t treat multiplication O(1) as the value grows exponentially. Also it takes significant space to store the result of factorial N!.

Count the number of Factor 5

If we think about it, the number of zeros are made by a pair of 5 and 2. And the number of 2s is far more than the number of 5s. Therefore, the number of trailing zeros is determined by the number of factor 5.

We can count it this way:

1
2
3
4
5
6
7
8

def trailingZeroes(n: int) -> int:        
    zero_count = 0
    for i in range(5, n + 1, 5):
        current = i
        while current % 5 == 0:
            zero_count += 1
            current //= 5
    return zero_count

def trailingZeroes(n: int) -> int:        
    zero_count = 0
    for i in range(5, n + 1, 5):
        current = i
        while current % 5 == 0:
            zero_count += 1
            current //= 5
    return zero_count

Alternatively, we keep tracking a multiple of 5.

1
2
3
4
5
6
7
8

def trailingZeroes(n: int) -> int:
    zero_count = 0
    for i in range(5, n + 1, 5):
        power_of_5 = 5
        while i % power_of_5 == 0:
            zero_count += 1
            power_of_5 *= 5
    return zero_count

def trailingZeroes(n: int) -> int:
    zero_count = 0
    for i in range(5, n + 1, 5):
        power_of_5 = 5
        while i % power_of_5 == 0:
            zero_count += 1
            power_of_5 *= 5
    return zero_count

The complexity is O(N). As the inner loop tends to amortizes to O(1). The most numbers contain a single factor of 5.

Count the number of Factor 5 Efficiently

The number of zeros for factorial N! is determined by number of 5’s and we can accumulate the 5’s in 25, 125, 625 .. as well.. Thus, the total number of 5’s can be computed via:

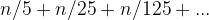
1
2
3
4
5
6
7

def trailingZeroes(n: int) -> int:
    zero_count = 0
    current_multiple = 5
    while n >= current_multiple:
        zero_count += n // current_multiple
        current_multiple *= 5
    return zero_count

def trailingZeroes(n: int) -> int:
    zero_count = 0
    current_multiple = 5
    while n >= current_multiple:
        zero_count += n // current_multiple
        current_multiple *= 5
    return zero_count

Alternatively, we can divide and count:

1
2
3
4
5
6

def trailingZeroes(n: int) -> int:
    zero_count = 0
    while n > 0:
        n //= 5
        zero_count += n
    return zero_count

def trailingZeroes(n: int) -> int:
    zero_count = 0
    while n > 0:
        n //= 5
        zero_count += n
    return zero_count

The time complexity is O(LogN).

See also: C/C++ Coding Exercise – Factorial Trailing Zeroes

–EOF (The Ultimate Computing & Technology Blog) —