Teaching Kids Programming – Recursive Algorithms to Compute the K-th Symbol in Grammar

Teaching Kids Programming: Videos on Data Structures and Algorithms

We build a table of n rows (1-indexed). We start by writing 0 in the 1st row. Now in every subsequent row, we look at the previous row and replace each occurrence of 0 with 01, and each occurrence of 1 with 10. For example, for n = 3, the 1st row is 0, the 2nd row is 01, and the 3rd row is 0110.

Given two integer n and k, return the kth (1-indexed) symbol in the nth row of a table of n rows.

Example 1:
Input: n = 1, k = 1
Output: 0
Explanation: row 1: 0

Example 2:
Input: n = 2, k = 1
Output: 0
Explanation:
row 1: 0
row 2: 01

Example 3:
Input: n = 2, k = 2
Output: 1
Explanation:
row 1: 0
row 2: 01

Constraints:
1 <= n <= 30
1 <= k <= 2n – 1

Algorithms to Compute the K-th Symbol in Grammar via Simulations

Recursive Algorithm to Compute the K-th Symbol in the Grammer

We know the process to construct the n-th Grammar, by replacing the 0 with “01” and 1 with “10” from (n-1)-th Grammer string, thus we can follow this process either iteratively or recursively.

The following is the recursive implementation of this algorithm – where the f(n) returns the n-th grammer string.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

class Solution:
    @cache
    def kthGrammar(self, n, k):
        @cache
        def f(n):
            if n == 1:
                return "0"
            last = f(n - 1)
            ans = ""
            for i in last:
                if i == "0":
                    ans += "01"
                else:
                    ans += "10"
            return ans
        return int(f(n)[k - 1])

class Solution:
    @cache
    def kthGrammar(self, n, k):
        @cache
        def f(n):
            if n == 1:
                return "0"
            last = f(n - 1)
            ans = ""
            for i in last:
                if i == "0":
                    ans += "01"
                else:
                    ans += "10"
            return ans
        return int(f(n)[k - 1])

Iterative Algorithm to Compute the K-th Symbol in the Grammer

And below is the iterative approach, where we compute and update the grammer string.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

class Solution:
    @cache
    def kthGrammar(self, n, k):
        cur = [0]
        for i in range(n):
            nt = []
            for x in cur:
                if x == 0:
                    nt.append(0)
                    nt.append(1)
                else:
                    nt.append(1)
                    nt.append(0)
            cur = nt
        return cur[k-1]

class Solution:
    @cache
    def kthGrammar(self, n, k):
        cur = [0]
        for i in range(n):
            nt = []
            for x in cur:
                if x == 0:
                    nt.append(0)
                    nt.append(1)
                else:
                    nt.append(1)
                    nt.append(0)
            cur = nt
        return cur[k-1]

Both implementations are not memory and time efficient because we have to generate and hold the string in the memory, and remember, the n-th string has 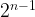characters.

Find the Pattern And Invert

We don’t actually need to generate the n-th string in order to find out the k-th character at n-th row. If the k-th is at the first half, we know from the pattern that it is equal to the same bit at previous row, otherwise, we can map to the first half and then invert it.

Recursion

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

class Solution:
    @cache
    def kthGrammar(self, n, k):
        # 0
        # 01
        # 0110
        # 01101001
        # 0110100110010110
 
        if n == 1 or k == 1:
            return 0       
        mid = 1<<(n-2)
        if k <= mid:
            return self.kthGrammar(n - 1, k)
        return 1 - self.kthGrammar(n - 1, k - mid)

class Solution:
    @cache
    def kthGrammar(self, n, k):
        # 0
        # 01
        # 0110
        # 01101001
        # 0110100110010110

        if n == 1 or k == 1:
            return 0       
        mid = 1<<(n-2)
        if k <= mid:
            return self.kthGrammar(n - 1, k)
        return 1 - self.kthGrammar(n - 1, k - mid)

The time complexity is O(N), and the space complexity is O(N) as well due to recursion calling stack, but we can tail recursive optimise it.

Iterative Implementation

A more efficient approach for this specific problem could be to use iteration or a non-recursive approach to determine the K-th symbol. The K-th symbol in the N-th row can be determined based on its position and its parent’s value in the previous row. This can be done iteratively, by tracing back from the K-th position in the N-th row to the first row, and determining whether each step involves a flip (1 to 0 or 0 to 1) or not. This approach would be more efficient in terms of both time and space complexity compared to a tail-recursive or even a regular recursive solution.

Here is an iterative version of the function:

1
2
3
4
5
6
7
8
9
10

class Solution:
    def kthGrammar(self, n, k):
        result = 0
        while n > 1:
            mid = 1 << (n - 2)
            if k > mid:
                result = 1 - result
                k -= mid
            n -= 1
        return result

class Solution:
    def kthGrammar(self, n, k):
        result = 0
        while n > 1:
            mid = 1 << (n - 2)
            if k > mid:
                result = 1 - result
                k -= mid
            n -= 1
        return result

This version iteratively reduces the problem’s size by moving up one row at a time and adjusting the position k as needed. The result variable is flipped whenever k is greater than mid, simulating the change from left child to right child in the binary tree representation of the grammar.

Tail Recursive Optimisation

To optimize the given recursive function using tail recursion, the main idea is to eliminate the need for additional stack frames for each recursive call. In the provided code, the recursive call depends on the return value of the recursive function itself, making it a non-tail recursive function.

To convert this into a tail-recursive function, we need to pass along additional arguments to carry the result of computations from one recursive call to the next. However, the nature of this specific problem (K-th symbol in Grammar) makes it challenging to directly apply tail recursion due to its inherent binary tree structure and the dependency on previous states.

To convert the given recursion to a tail recursive form, we need to change the structure of the recursion such that the last operation in each recursive call is the recursive call itself. However, the nature of this problem (K-th symbol in Grammar) involves a branching logic that makes it challenging to directly apply a tail recursive approach without fundamentally altering the logic of the function.

In many languages, including Python, tail recursion optimization is not inherently supported, which means that even tail recursive functions can lead to a stack overflow for deep recursive calls. Python does not optimize tail recursion, so using an iterative approach is often more efficient and safer for deep recursions.

That being said, here’s an attempt to rewrite the function in a more tail-recursive manner, though it’s important to note that this won’t yield the performance benefits of tail recursion seen in languages that support tail call optimization:

1
2
3
4
5
6
7
8
9

class Solution:
    @cache
    def kthGrammar(self, n, k, acc=0):
        if n == 1 or k == 1:
            return acc
        mid = 1 << (n - 2)
        if k <= mid:
            return self.kthGrammar(n - 1, k, acc)
        return self.kthGrammar(n - 1, k - mid, 1 - acc)

class Solution:
    @cache
    def kthGrammar(self, n, k, acc=0):
        if n == 1 or k == 1:
            return acc
        mid = 1 << (n - 2)
        if k <= mid:
            return self.kthGrammar(n - 1, k, acc)
        return self.kthGrammar(n - 1, k - mid, 1 - acc)

In this version, an accumulator acc is passed along each recursive call to hold the result. The last operation in the recursive function is now the recursive call itself, making it tail recursive. However, as mentioned before, Python doesn’t optimize tail recursion, so this change is more of a theoretical exercise in tail recursion rather than a practical optimization in Python.

–EOF (The Ultimate Computing & Technology Blog) —