Teaching Kids Programming – Largest Sum of Non-Adjacent Numbers (2D Version – Disappearing Coins in a Matrix)

Teaching Kids Programming: Videos on Data Structures and Algorithms

You are given a two-dimensional list of integers matrix where each matrix[r][c] represents the number of coins in that cell. When you pick up coins on matrix[r][c], all the coins on row r – 1 and r + 1 disappear, as well as the coins at the two cells matrix[r][c + 1] and matrix[r][c – 1]. Return the maximum number of coins that you can collect.

Constraints
n, m ≤ 250 where n and m are the number of rows and columns in matrix
Example 1
Input

1 2 3 4 5

matrix = [     [1, 7, 6, 5],     [9, 9, 3, 1],     [4, 8, 1, 2] ]

matrix = [
    [1, 7, 6, 5],
    [9, 9, 3, 1],
    [4, 8, 1, 2]
]

Output
22
Explanation
We can pick cells with the coins 7, 5, and 8 and 2.

Hints:
You cannot take two adjacent rows/cols. Does this sound familiar?
Solve the problem for each single row and get maximum points for each row, then create a new array with these values and perform the same operation on the new array

Largest Sum of Non-Adjacent Numbers in a Matrix via Dynamic Programming Algorithm

The 1D version of this problem: maximize the sum of non-adjacent numbers (when we pick i-th number, two numbers next to it (i-1, i+1) disappear). We can solve this via Dynamic Programming Algorithm:

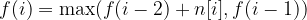
Base conditions: 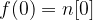and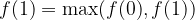

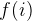represents the maximum sum we can get for numbers up to index i (inclusive) aka n[:i+1].

We can implement this in a few ways: Top Down Dynamic Programming (Recursion via Memoization aka the @cache keyword to use hash table to store):

1
2
3
4
5
6
7
8
9
10
11
12
13
14

def f(nums):
    n = len(nums)
    if n == 0:
        return 0
    
    @cache
    def g(i):
        if i == 0:
            return nums[0]
        if i == 1:
            return max(nums[0], nums[1])
        return max(g(i - 2) + nums[i], g(i - 1))
     
    return g(len(nums) - 1)

def f(nums):
    n = len(nums)
    if n == 0:
        return 0
    
    @cache
    def g(i):
        if i == 0:
            return nums[0]
        if i == 1:
            return max(nums[0], nums[1])
        return max(g(i - 2) + nums[i], g(i - 1))
     
    return g(len(nums) - 1)

We can use the Bottom Up to implement the Dynamic Programming Equation, specifically using array to store the DP values:

1
2
3
4
5
6
7
8
9
10
11
12

def f(nums):
    n = len(nums)
    if not n:
        return 0 
    if n == 1:
        return nums[0]
    if n == 2:
        return max(nums)
    dp = [nums[0], max(nums[0], nums[1])]
    for i in range(2, n):
        dp.append(max(dp[-2] + nums[i], dp[-1]))
    return dp[-1]

def f(nums):
    n = len(nums)
    if not n:
        return 0 
    if n == 1:
        return nums[0]
    if n == 2:
        return max(nums)
    dp = [nums[0], max(nums[0], nums[1])]
    for i in range(2, n):
        dp.append(max(dp[-2] + nums[i], dp[-1]))
    return dp[-1]

And, similar to Fibonacci Numbers, we only need to keep the previous 2 items, and thus we can optimize the space to O(1):

1
2
3
4
5
6
7
8
9
10

def f(nums):
    n = len(nums)
    if n == 0:
        return 0
    if n == 1:
        return nums[0]
    a, b = 0, 0
    for i in nums:
        a, b = b, max(a + i, b)
    return b

def f(nums):
    n = len(nums)
    if n == 0:
        return 0
    if n == 1:
        return nums[0]
    a, b = 0, 0
    for i in nums:
        a, b = b, max(a + i, b)
    return b

With this f function() to solve the 1-D version, we then obtain the list of numbers aka largest sums for each row, and since all the numbers at neighbouring rows disappear, row-1 and row+1, it means that we can apply again the f function to return the largest sum.

1

return f([f(x) for x in M])

return f([f(x) for x in M])

The overall time complexity is O(RC) where R is the number of rows, and C is the number of columns respectively, and the space complexity (if we have the optimal implementation of the last f function which has O(1) space), is O(R) as we need to obtain the 1-D largest sum for each row, and store them in an array before we apply again the f function to it.

Largest Sum of Non-Adjacent Numbers (House Robber or Disappearing Coins): Dynamic Programming Algorithms

• Teaching Kids Programming – Dynamic Programming Algorithms to Compute the Maximum Non-Adjacent Tree Sum
• C++ Coding Exercise – House Robber II (Dynamic Programming)
• How to Maxmize Profits to Robbering in a Binary Tree using Dynamic Programming Algorithm?
• Using the Dynamic Programming Algorithm, the Depth First Search or Breadth First Search to Solve House Robber Problem
• Teaching Kids Programming – Largest Sum of Non-Adjacent Numbers (2D Version – Disappearing Coins in a Matrix)

–EOF (The Ultimate Computing & Technology Blog) —