Teaching Kids Programming – Max Profit of Rod Cutting (Unbounded Knapsack) via Bottom Up Dynamic Programming Algorithm

Teaching Kids Programming: Videos on Data Structures and Algorithms

You are given a list of integers prices where prices[i] represents the price to sell a rod of size i + 1, and an integer n which represents the current size of the rod.

Given you can cut the rod into any number of different sizes, return the maximum profit that can be earned.

Constraints
m = n ≤ 1000 where m is the length of prices.
Example 1
Input
prices = [1, 3, 5, 7, 7, 7]
n = 6
Output
10
Explanation
The price table shows that we can:
Sell a rod of size 1 for price of 1
Sell a rod of size 2 for price of 3
Sell a rod of size 3 for price of 5
Sell a rod of size 4 for price of 7
Sell a rod of size 5 for price of 7
Sell a rod of size 6 for price of 7
The optimal way to cut the rod is to split it into 2 pieces of length 3, to achieve profit of 10.

Max Profit of Rod Cutting (Unbounded Knapsack) via Bottom Up Dynamic Programming Algorithm

This is a unbounded knapsack problem. There are 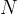items, which are size 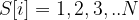. And the values for each items is 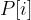. Given the size 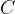of the knapsack, we want to choose the items such that the total values is maximized.

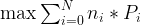subject to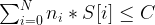
The 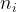is the count of the item i and we can have as many as we want for each item.

We can use Top Down Dynamic Programming aka Recursion with Memoization where we add @cache to let the computer memorize the values for us. Alternatively, we can use Bottom Up Dynamic Programming algorithm to solve this via the arrays where we proactively store/remember the values.

1
2
3
4
5
6
7

class Solution:
    def maxProfitUnboundedKnapsack(self, prices, n):        
        dp = [0] * (n + 1)
        for i in range(1, n + 1):
            for j in range(i):
                dp[i] = max(dp[i], prices[j] + dp[i - j - 1])
        return dp[-1]

class Solution:
    def maxProfitUnboundedKnapsack(self, prices, n):        
        dp = [0] * (n + 1)
        for i in range(1, n + 1):
            for j in range(i):
                dp[i] = max(dp[i], prices[j] + dp[i - j - 1])
        return dp[-1]

The time complexity is O(N^2) quadratic (e.g. polynomial time). The outer loop i takes N iterations, and the inner loop takes up to i so overall iterations are N+(N-1)+(N-2)+… which is N(N+1)//2 thus O(N^2).

The space complexity is O(N) as we need one additional array to store the DP values e.g. dp[0] to dp[n].

See also this where we can solve this unbouned knapsack problem via Top Down Dynamic Programming Algorithm aka Recursion with Memoization (@cache): Teaching Kids Programming – Max Profit of Rod Cutting (Unbounded Knapsack) via Top Down Dynamic Programming Algorithm

Knapsack Problems

• Teaching Kids Programming - 0/1 Knapsack: Length of the Longest Subsequence That Sums to Target (Recursion+Memoization=Top Down Dynamic Programming)
• Teaching Kids Programming - 0/1 Knapsack Space Optimised Dynamic Programming Algorithm
• Teaching Kids Programming - Using Bottom Up Dynamic Programming Algorithm to Solve 0/1 Knapsack Problem
• Teaching Kids Programming - 0/1 Knapsack Problem via Top Down Dynamic Programming Algorithm
• Teaching Kids Programming - Multiple Strange Coin Flips/Toss Bottom Up Dynamic Programming Algorithm (Knapsack Variant)
• Teaching Kids Programming - Multiple Strange Coin Flips/Toss Top Down Dynamic Programming Algorithm (Knapsack Variant)
• Teaching Kids Programming - Max Profit of Rod Cutting (Unbounded Knapsack) via Bottom Up Dynamic Programming Algorithm
• Teaching Kids Programming - Max Profit of Rod Cutting (Unbounded Knapsack) via Top Down Dynamic Programming Algorithm
• Teaching Kids Programming - Brick Layout (Unlimited Knapsack) via Bottom Up Dynamic Programming Algorithm
• Teaching Kids Programming - Brick Layout (Unlimited Knapsack) via Top Down Dynamic Programming Algorithm
• Count Multiset Sum (Knapsacks) by Dynamic Programming Algorithm
• Count Multiset Sum (Knapsacks) by Recursive BackTracking Algorithm
• Dynamic Programming Algorithm to Solve the Poly Knapsack (Ubounded) Problem
• Dynamic Programming Algorithm to Solve 0-1 Knapsack Problem
• Classic Unlimited Knapsack Problem Variant: Coin Change via Dynamic Programming and Depth First Search Algorithm
• Classic Knapsack Problem Variant: Coin Change via Dynamic Programming and Breadth First Search Algorithm
• Complete Knapsack Problem
• 0/1 Knapsack Problem
• Teaching Kids Programming - Combination Sum Up to Target (Unique Numbers) by Dynamic Programming Algorithms
• Algorithms Series: 0/1 BackPack - Dynamic Programming and BackTracking
• Using BackTracking Algorithm to Find the Combination Integer Sum
• Facing Heads Probabilties of Tossing Strange Coins using Dynamic Programming Algorithm
• Partition Equal Subset Sum Algorithms using DFS, Top-Down and Bottom-up DP

–EOF (The Ultimate Computing & Technology Blog) —