Algorithms to Locate the Leftmost Column with at Least a One in a Binary Matrix

A binary matrix means that all elements are 0 or 1. For each individual row of the matrix, this row is sorted in non-decreasing order. Given a row-sorted binary matrix binaryMatrix, return leftmost column index(0-indexed) with at least a 1 in it. If such index doesn’t exist, return -1.

You can’t access the Binary Matrix directly. You may only access the matrix using a BinaryMatrix interface:

• BinaryMatrix.get(row, col) returns the element of the matrix at index (row, col) (0-indexed).
• BinaryMatrix.dimensions() returns a list of 2 elements [rows, cols], which means the matrix is rows * cols.

For custom testing purposes you’re given the binary matrix mat as input in the following four examples. You will not have access the binary matrix directly.

Example 1:
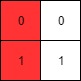
Input: mat = [[0,0],[1,1]]
Output: 0

Example 2:
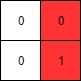
Input: mat = [[0,0],[0,1]]
Output: 1

Example 3:
Input: mat = [[0,0],[0,0]]
Output: -1

Example 4:
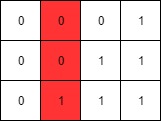
Input: mat = [[0,0,0,1],[0,0,1,1],[0,1,1,1]]
Output: 1

Constraints:
rows == mat.length
cols == mat[i].length
1 <= rows, cols <= 100
mat[i][j] is either 0 or 1.
mat[i] is sorted in a non-decreasing way.

Hints:

• (Binary Search) For each row do a binary search to find the leftmost one on that row and update the answer.
• (Optimal Approach) Imagine there is a pointer p(x, y) starting from top right corner. p can only move left or down. If the value at p is 0, move down. If the value at p is 1, move left. Try to figure out the correctness and time complexity of this algorithm.

Bruteforce Algorithm to Locate the Left-most 1-column in a Binary Matrix

We can iterate over the matrix in O(MN) time and record the smallest column when we have a one in the binary matrix. The algorithm does not utilise the fact that the binary matrix is sorted in both columns and rows.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

/**
 * // This is the BinaryMatrix's API interface.
 * // You should not implement it, or speculate about its implementation
 * class BinaryMatrix {
 *   public:
 *     int get(int x, int y);
 *     vector<int> dimensions();
 * };
 */
 
class Solution {
public:
    int leftMostColumnWithOne(BinaryMatrix &binaryMatrix) {
        vector<int> dim = binaryMatrix.dimensions();
        int row = dim[0];
        int col = dim[1];
        int res = INT_MAX;
        for (int i = 0; i < row; ++ i) {
            for (int j = 0; j < col; ++ j) {
                if (binaryMatrix.get(i, j) == 1) {
                    res = min(res, j);
                }
            }
        }   
        return res == INT_MAX ? -1 : res;
    }
};

/**
 * // This is the BinaryMatrix's API interface.
 * // You should not implement it, or speculate about its implementation
 * class BinaryMatrix {
 *   public:
 *     int get(int x, int y);
 *     vector<int> dimensions();
 * };
 */

class Solution {
public:
    int leftMostColumnWithOne(BinaryMatrix &binaryMatrix) {
        vector<int> dim = binaryMatrix.dimensions();
        int row = dim[0];
        int col = dim[1];
        int res = INT_MAX;
        for (int i = 0; i < row; ++ i) {
            for (int j = 0; j < col; ++ j) {
                if (binaryMatrix.get(i, j) == 1) {
                    res = min(res, j);
                }
            }
        }   
        return res == INT_MAX ? -1 : res;
    }
};

Locate the Left-most Column using Binary Search Algorithm

A better approach is to iterate over the rows, and binary search the left-most 1 since the rows are sorted. The time complexity is O(MLogN) where M is the number of the rows, and N is the number of the columns of the matrix.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

/**
 * // This is the BinaryMatrix's API interface.
 * // You should not implement it, or speculate about its implementation
 * class BinaryMatrix {
 *   public:
 *     int get(int x, int y);
 *     vector<int> dimensions();
 * };
 */
 
class Solution {
public:
    int leftMostColumnWithOne(BinaryMatrix &binaryMatrix) {
        vector<int> dim = binaryMatrix.dimensions();
        int row = dim[0];
        int col = dim[1];
        int res = INT_MAX;        
        for (int r = 0; r < row; ++ r) {
            int a = 0, b = col - 1;
            while (a <= b) {
                int mid = a + (b - a) / 2;
                if (binaryMatrix.get(r, mid) == 1) {
                    b = mid - 1;
                    res = min(res, mid);
                } else {
                    a = mid + 1;
                }
            }
        }
        return res == INT_MAX ? -1 : res;
    }
};

/**
 * // This is the BinaryMatrix's API interface.
 * // You should not implement it, or speculate about its implementation
 * class BinaryMatrix {
 *   public:
 *     int get(int x, int y);
 *     vector<int> dimensions();
 * };
 */

class Solution {
public:
    int leftMostColumnWithOne(BinaryMatrix &binaryMatrix) {
        vector<int> dim = binaryMatrix.dimensions();
        int row = dim[0];
        int col = dim[1];
        int res = INT_MAX;        
        for (int r = 0; r < row; ++ r) {
            int a = 0, b = col - 1;
            while (a <= b) {
                int mid = a + (b - a) / 2;
                if (binaryMatrix.get(r, mid) == 1) {
                    b = mid - 1;
                    res = min(res, mid);
                } else {
                    a = mid + 1;
                }
            }
        }
        return res == INT_MAX ? -1 : res;
    }
};

When we find a One, we immediately update the smallest column and search in the lower half.

Optimal Solution by Moving the Coodinate to Lower Left

If we start from the top right corner, move left if it is 1, otherwise move down. When the position is out of the dimensions, we know the smallest column is one to the right.

The complexity is O(M + N).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

/**
 * // This is the BinaryMatrix's API interface.
 * // You should not implement it, or speculate about its implementation
 * class BinaryMatrix {
 *   public:
 *     int get(int x, int y);
 *     vector<int> dimensions();
 * };
 */
 
class Solution {
public:
    int leftMostColumnWithOne(BinaryMatrix &binaryMatrix) {
        vector<int> dim = binaryMatrix.dimensions();
        int row = dim[0];
        int col = dim[1];
        int r = 0;
        int c = col - 1;
        while ((r < row) && (c >= 0)) {
            if (binaryMatrix.get(r, c) == 0) {
                r ++;
            } else {
                c --;
            }
        }
        return c + 1 == col ? -1 : c + 1;
    }
};

/**
 * // This is the BinaryMatrix's API interface.
 * // You should not implement it, or speculate about its implementation
 * class BinaryMatrix {
 *   public:
 *     int get(int x, int y);
 *     vector<int> dimensions();
 * };
 */

class Solution {
public:
    int leftMostColumnWithOne(BinaryMatrix &binaryMatrix) {
        vector<int> dim = binaryMatrix.dimensions();
        int row = dim[0];
        int col = dim[1];
        int r = 0;
        int c = col - 1;
        while ((r < row) && (c >= 0)) {
            if (binaryMatrix.get(r, c) == 0) {
                r ++;
            } else {
                c --;
            }
        }
        return c + 1 == col ? -1 : c + 1;
    }
};

If current value is 1, we know the answer is at most current column, thus we move left. It is zero, we try current column to see if it has 1. The lower-right half of the matrix may contain ones.

–EOF (The Ultimate Computing & Technology Blog) —