C++ Coding Exercise: How to Check if a Large Integer is divisible by 11?

We all know that the 32-bit signed/unsigned integer takes 4 byte while 64-bit signed/unsigned integer takes 8 bytes to store. If there is a very big integer which is stored by a string e.g. “1234123412341289759687893247874” certainly we cannot hold this value exactly using the primitive data types. This article will show you a quick method to check if any large integer can be divided by 11.

A little Math

We have this integer: 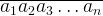, so mathematically it can be expressed as: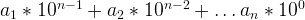

We know that 1, 100, 10000, 100000, .. 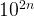modular 11 has the remainder 1 and 10, 1000, 100000… 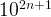modular 11 has the remainder -1.

Therefore, if n is odd: 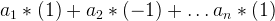otherwise: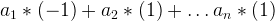

So, to sum up, we just need to check the alternating sum of the digits: 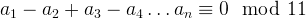to see if the sum (of course smaller and can be hold by primitive data types) can be divisible by 11.

For example, 3619 can by devisible by 11 because +3-6+1-9=-11 which is divisible by 11.

C++ Code

So, the following is the C++ code implementation based on the above idea and the STL::string type.

1
2
3
4
5
6
7
8
9

bool DivBy11(string num) {
    int sign = 1;
    int sum = 0;
    for (int i = 0; i < num.length(); i ++) {
        sum += (sign) * (num[i] - 48);
        sign *= -1;
    }
    return sum % 11 == 0;
}

bool DivBy11(string num) {
    int sign = 1;
    int sum = 0;
    for (int i = 0; i < num.length(); i ++) {
        sum += (sign) * (num[i] - 48);
        sign *= -1;
    }
    return sum % 11 == 0;
}

–EOF (The Ultimate Computing & Technology Blog) —