GCD and LCM

GCD (Greatest Common Divisor), in mathematics, is refered to the largest number that divides two or more non-zero integers without a remainder. For example, the GCD of 8 and 12 is 4.

LCM (Least Common Multiple), in mathematics, is the smallest positive number that is a multiple of both numbers. For example, the LCM of 8 and 12 is 24.

The releation between GCD and LCM is the following:

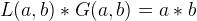
A popular algorithm in math, to compute the GCD is called Euclidean Algorithm, which iteratively substracts the small number from a larger one. This can be defined in the following python code:

1
2
3
4
5
6
7
8
9

def gcd(a, b):
    if a == 0:
        return b
    while b:
        if a > b:
            a -= b
        else:
            b -= a
    return a

def gcd(a, b):
    if a == 0:
        return b
    while b:
        if a > b:
            a -= b
        else:
            b -= a
    return a

The recurisve implementation is shorter, and can be found below:

1
2
3
4

def gcd(a, b):
    if b == 0:
        return a
    return gcd(b, a % b)

def gcd(a, b):
    if b == 0:
        return a
    return gcd(b, a % b)

A more efficient implementation using non-recursive structure in Python is as follows:

1
2
3
4

def gcd(a, b):
    while b:
        a, b = b, a % b
    return a

def gcd(a, b):
    while b:
        a, b = b, a % b
    return a

It is noted that

1

a, b = b, a % b

a, b = b, a % b

is to swap a and b with the new values b and the remainder of a / b.

–EOF (The Ultimate Computing & Technology Blog) —