How to Construct Minimum Spanning Tree using Kruskal or Breadth First Search Algorithm?

There are N cities numbered from 1 to N.

You are given connections, where each connections[i] = [city1, city2, cost] represents the cost to connect city1 and city2 together. (A connection is bidirectional: connecting city1 and city2 is the same as connecting city2 and city1.)

Return the minimum cost so that for every pair of cities, there exists a path of connections (possibly of length 1) that connects those two cities together. The cost is the sum of the connection costs used. If the task is impossible, return -1.

three-nodes

Example 1:
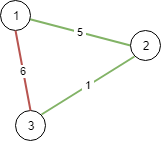
Input: N = 3, connections = [[1,2,5],[1,3,6],[2,3,1]]
Output: 6
Explanation:
Choosing any 2 edges will connect all cities so we choose the minimum 2.

two-edges

Example 2:
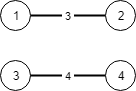
Input: N = 4, connections = [[1,2,3],[3,4,4]]
Output: -1
Explanation:
There is no way to connect all cities even if all edges are used.

Note:

1 <= N <= 10000

1 <= connections.length <= 10000

1 <= connections[i][0], connections[i][1] <= N

0 <= connections[i][2] <= 10^5

connections[i][0] != connections[i][1]

Hints:

What if we model the cities as a graph?

Build a graph of cities and find the minimum spanning tree.

You can use a variation of the Kruskal’s algorithm for that.

Sort the edges by their cost and use a union-find data structure.

How to check all cities are connected?

At the beginning we have n connected components, each time we connect two components the number of connected components is reduced by one. At the end we should end with only a single component otherwise return -1.

What is a Minimum Spanning Tree?

In a unidirected and weighted Graph, the vertices/nodes are connected with different weights, a minimum spanning tree or MST is the tree that contains all the nodes in the original graph and at the meantime, the sum of the weights for the edges are minimum.

The MST is a great tool/algorithm to solve many graph-related problems such as Learning Languages.

Intuitive Algorithm to Build Minimum Spanning Tree

We can have one vector/set to record the current chosen nodes which we can put any node to start. Another set or vector is used to keep tracking of the remaining nodes. The following algorithm runs at O(N^2) which it will repeatedly choose a minimum weighted edge between two sets/vectors, update the total cost, and remove the node from the remaining set.

The input connections represents the graph using the linked-list, which can be easily converted to adjacent matrix using two dimension array.

class Solution {
public:
    int minimumCost(int N, vector<vector<int>>& conections) {
        vector<vector<int>> f(N + 1, vector<int>(N + 1, INT_MAX));
        // convert to adjacent matrix
        for (const auto &n: conections) {
            f[n[0]][n[1]] = n[2];
            f[n[1]][n[0]] = n[2];
        }
        vector<int> cur(1, 1);
        vector<int> left;
        int ans = 0;
        // remaining set
        for (int i = 2; i <= N; ++ i) left.push_back(i);
        while (left.size() > 0) {
            int cost = INT_MAX;
            int idx = -1;
            // pick the shortest edge between nodes in two sets        
            for (int i = 0; i < left.size(); ++ i) {
                for (int j = 0; j < cur.size(); ++ j) {
                    if (f[left[i]][cur[j]] < cost) {
                        cost = f[left[i]][cur[j]];
                        idx = i;
                    }
                }
            }
            // the graph is not connected
            if (cost == INT_MAX) return -1;
            cur.push_back(left[idx]);
            ans += cost;
            // remove the chosen node from the remaining set
            left.erase(begin(left) + idx);
        }
        return ans;
    }
};

class Solution {
public:
    int minimumCost(int N, vector<vector<int>>& conections) {
        vector<vector<int>> f(N + 1, vector<int>(N + 1, INT_MAX));
        // convert to adjacent matrix
        for (const auto &n: conections) {
            f[n[0]][n[1]] = n[2];
            f[n[1]][n[0]] = n[2];
        }
        vector<int> cur(1, 1);
        vector<int> left;
        int ans = 0;
        // remaining set
        for (int i = 2; i <= N; ++ i) left.push_back(i);
        while (left.size() > 0) {
            int cost = INT_MAX;
            int idx = -1;
            // pick the shortest edge between nodes in two sets        
            for (int i = 0; i < left.size(); ++ i) {
                for (int j = 0; j < cur.size(); ++ j) {
                    if (f[left[i]][cur[j]] < cost) {
                        cost = f[left[i]][cur[j]];
                        idx = i;
                    }
                }
            }
            // the graph is not connected
            if (cost == INT_MAX) return -1;
            cur.push_back(left[idx]);
            ans += cost;
            // remove the chosen node from the remaining set
            left.erase(begin(left) + idx);
        }
        return ans;
    }
};

As we can see, the above C++ implementation is slow, because it is O(N^2) and also the use of the vector is slow when you want to remove an element in the vector. We can slightly improve this by using a list in C++, which is based on the doubly-linked data structure – O(1) to insert or remove an element in the list compared to O(N) in a vector.

class Solution {
public:
    int minimumCost(int N, vector<vector<int>>& conections) {
        vector<vector<int>> f(N + 1, vector<int>(N + 1, INT_MAX));
        // convert to adjacent matrix to represent the graph
        for (const auto &n: conections) {
            f[n[0]][n[1]] = n[2];
            f[n[1]][n[0]] = n[2];
        }
        // start with node 1
        vector<int> cur(1, 1);
        // the remaining nodes
        list<int> left;
        int ans = 0;
        for (int i = 2; i <= N; ++ i) left.push_back(i);
        while (left.size() > 0) { // when there is still node not being connected
            int cost = INT_MAX;
            list<int>::iterator idx;
            for (auto n = left.begin(); n != left.end(); ++ n) {
                for (int j = 0; j < cur.size(); ++ j) {
                    if (f[*n][cur[j]] < cost) {
                        cost = f[*n][cur[j]];
                        idx = n;
                    }
                }
            }
            // the graph is not connected
            if (cost == INT_MAX) return -1;
            cur.push_back(*idx);
            ans += cost;
            // erase the node from remaining set O(1)
            left.erase(idx);
        }
        return ans;
    }
};

class Solution {
public:
    int minimumCost(int N, vector<vector<int>>& conections) {
        vector<vector<int>> f(N + 1, vector<int>(N + 1, INT_MAX));
        // convert to adjacent matrix to represent the graph
        for (const auto &n: conections) {
            f[n[0]][n[1]] = n[2];
            f[n[1]][n[0]] = n[2];
        }
        // start with node 1
        vector<int> cur(1, 1);
        // the remaining nodes
        list<int> left;
        int ans = 0;
        for (int i = 2; i <= N; ++ i) left.push_back(i);
        while (left.size() > 0) { // when there is still node not being connected
            int cost = INT_MAX;
            list<int>::iterator idx;
            for (auto n = left.begin(); n != left.end(); ++ n) {
                for (int j = 0; j < cur.size(); ++ j) {
                    if (f[*n][cur[j]] < cost) {
                        cost = f[*n][cur[j]];
                        idx = n;
                    }
                }
            }
            // the graph is not connected
            if (cost == INT_MAX) return -1;
            cur.push_back(*idx);
            ans += cost;
            // erase the node from remaining set O(1)
            left.erase(idx);
        }
        return ans;
    }
};

However, algorithm-wise, it is still too slow, remember this is O(N^2) time, can we do any better?

Kruskal’s Algorithm to Connect the Nodes With Minimum Cost

Kruskal’s Algorithm can be implemented using the Disjoint Set. At the begining, all nodes are classified as an individual group. And we sort the edges/connections in the ascending weighted order.

Then, we pick the edge from the smallest to the largest, union the nodes if they are not connected, and update the total cost. At the end, if there is only a single group, we return the total cost, otherwise -1.

class Solution {
public:
    int minimumCost(int N, vector<vector<int>>& connections) {
        int totalCost = 0;
        vector<int> parent(N + 1);
        for (int i = 0; i <= N;  ++ i) {
            parent[i] = i; // initial node group identifier
        }
        sort(begin(connections), end(connections), [](auto &a, auto &b) {
            return a[2] < b[2];
        });
        for (const auto &c: connections) {
            int x = c[0];
            int y = c[1];
            if (!connected(x, y, parent)) {
                union_sets(x, y, parent);
                totalCost += c[2];
            }
        }
        int c = 0;
        for (int i = 1; i <= N; ++ i) {
            if (parent[i] == i) {
                c ++;
            }
        }
        return c == 1 ? totalCost : -1;
    }
    
private:
    // if parents of both nodes are the same, they are connected
    bool connected(int x, int y, vector<int> &parent) {
        return find(x, parent) == find(y, parent);
    }
    
    // return the parent identifier of a node
    int find(int x, vector<int> &parent) {
        while (parent[x] != x) {
            parent[x] = parent[parent[x]]; // compress the path
            x = parent[x];
        }
        return x;
    }
    
    // set the parent of x to y if they are not the same
    void union_sets(int x, int y, vector<int> &parent) {
        int px = find(x, parent);
        int py = find(y, parent);        
        if (px != py) {
            parent[px] = py;
        }
    }
};

class Solution {
public:
    int minimumCost(int N, vector<vector<int>>& connections) {
        int totalCost = 0;
        vector<int> parent(N + 1);
        for (int i = 0; i <= N;  ++ i) {
            parent[i] = i; // initial node group identifier
        }
        sort(begin(connections), end(connections), [](auto &a, auto &b) {
            return a[2] < b[2];
        });
        for (const auto &c: connections) {
            int x = c[0];
            int y = c[1];
            if (!connected(x, y, parent)) {
                union_sets(x, y, parent);
                totalCost += c[2];
            }
        }
        int c = 0;
        for (int i = 1; i <= N; ++ i) {
            if (parent[i] == i) {
                c ++;
            }
        }
        return c == 1 ? totalCost : -1;
    }
    
private:
    // if parents of both nodes are the same, they are connected
    bool connected(int x, int y, vector<int> &parent) {
        return find(x, parent) == find(y, parent);
    }
    
    // return the parent identifier of a node
    int find(int x, vector<int> &parent) {
        while (parent[x] != x) {
            parent[x] = parent[parent[x]]; // compress the path
            x = parent[x];
        }
        return x;
    }
    
    // set the parent of x to y if they are not the same
    void union_sets(int x, int y, vector<int> &parent) {
        int px = find(x, parent);
        int py = find(y, parent);        
        if (px != py) {
            parent[px] = py;
        }
    }
};

In the find function, we use the following to compress the paths:

1	parent[x] = parent[parent[x]];

parent[x] = parent[parent[x]];

Practically, the above C++ implementation of disjoint set is O(NlogN).

Breadth First Search Algorithm to Connect the Nodes With Minimum Cost

We can do a customize BFS (Breadth First Search) algorithm that is based on a priority queue. When an element is dequed, it is also the smallest edge. The graph is represented by adjacent matrix, where for simplicity, the weight value is listed as the first of the pair.

We need also to remember the visited node so they don’t get picked twice. And once a node is selected, we also need to push its children (connected edges) to the priority queue.

class Solution {
public:
    int minimumCost(int N, vector<vector<int>>& connections) {
        int mincost = 0;
        vector<vector<pair<int, int>>> g(N + 1);
        vector<bool> vis(N + 1);
        for (const auto &c: connections) {
            g[c[0]].push_back({ c[2], c[1] });
            g[c[1]].push_back({ c[2], c[0] });
        }
        auto cmp = [](pair<int, int> a, pair<int, int> b) {
            return a.first > b.first;
        };
        priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(cmp)> q(cmp);
        q.push({0, 1}); // start with city 1, cost = 0
        while(!q.empty()) {
            int x = q.top().second; // city
            int w = q.top().first;  // cost
            q.pop();
            if(vis[x]) continue;
            mincost += w;
            vis[x] = true;
            // expand the connections
            for(int i = 0, sz = g[x].size(); i < sz; i++) {
                if (!vis[g[x][i].second]) {
                    q.push(g[x][i]);
                }
            }
        }
        for (int i = 1; i <= N; i++) {
                if (!vis[i]) return -1;
        }
        return mincost;
    }
};

class Solution {
public:
    int minimumCost(int N, vector<vector<int>>& connections) {
        int mincost = 0;
        vector<vector<pair<int, int>>> g(N + 1);
        vector<bool> vis(N + 1);
        for (const auto &c: connections) {
            g[c[0]].push_back({ c[2], c[1] });
            g[c[1]].push_back({ c[2], c[0] });
        }
        auto cmp = [](pair<int, int> a, pair<int, int> b) {
            return a.first > b.first;
        };
        priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(cmp)> q(cmp);
        q.push({0, 1}); // start with city 1, cost = 0
        while(!q.empty()) {
            int x = q.top().second; // city
            int w = q.top().first;  // cost
            q.pop();
            if(vis[x]) continue;
            mincost += w;
            vis[x] = true;
            // expand the connections
            for(int i = 0, sz = g[x].size(); i < sz; i++) {
                if (!vis[g[x][i].second]) {
                    q.push(g[x][i]);
                }
            }
        }
        for (int i = 1; i <= N; i++) {
                if (!vis[i]) return -1;
        }
        return mincost;
    }
};

The following specifies a customize comparator for the priority queue to use when deque elements.

auto cmp = [](pair<int, int> a, pair<int, int> b) {
   return a.first > b.first;
};
priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(cmp)> q(cmp);

auto cmp = [](pair<int, int> a, pair<int, int> b) {
   return a.first > b.first;
};
priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(cmp)> q(cmp);

However, it can be simply replaced by the std::greater, which will compare the first element of a pair by default.

1	priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int,int>>> q;

priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int,int>>> q;

The time complexity is O(NLogN) where N is the number of nodes in the graph. The space complexity is O(Max(N, C)) where C is the number of connections.

–EOF (The Ultimate Computing & Technology Blog) —

GD Star Rating
loading...

1767 words
Last Post: Two Pointer and Sliding Window Algorithm to Find K-Length Substrings With No Repeated Characters
Next Post: How to Find the Most Common Word in a String with a Banned List?

The Permanent URL is: How to Construct Minimum Spanning Tree using Kruskal or Breadth First Search Algorithm?

Algorithms, Blockchain and Cloud

How to Construct Minimum Spanning Tree using Kruskal or Breadth First Search Algorithm?

What is a Minimum Spanning Tree?

Intuitive Algorithm to Build Minimum Spanning Tree

Kruskal’s Algorithm to Connect the Nodes With Minimum Cost

Breadth First Search Algorithm to Connect the Nodes With Minimum Cost

Leave a Reply

What is a Minimum Spanning Tree?

Intuitive Algorithm to Build Minimum Spanning Tree

Kruskal’s Algorithm to Connect the Nodes With Minimum Cost

Breadth First Search Algorithm to Connect the Nodes With Minimum Cost

Related posts:

Leave a Reply