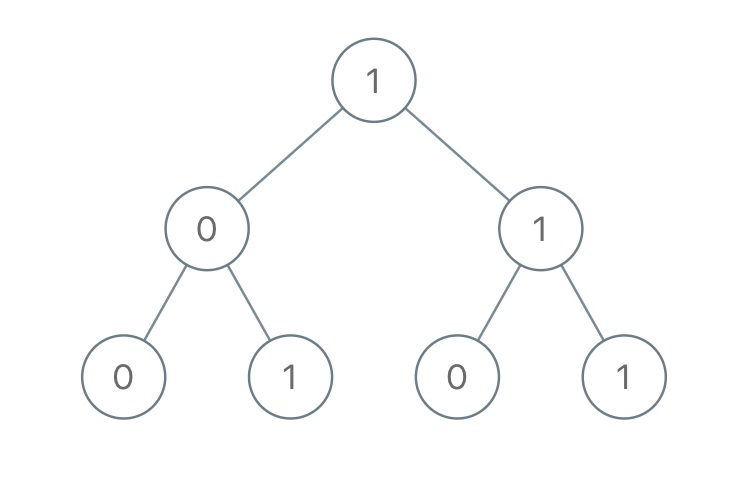
Given a binary tree, each node has value 0 or 1. Each root-to-leaf path represents a binary number starting with the most significant bit. For example, if the path is 0 – 1 – 1 – 0 – 1, then this could represent 01101 in binary, which is 13. For all leaves in the tree, consider the numbers represented by the path from the root to that leaf. Return the sum of these numbers.
Example 1:
Input: [1,0,1,0,1,0,1]
Output: 22
Explanation: (100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22Note:
The number of nodes in the tree is between 1 and 1000.
node.val is 0 or 1.
The answer will not exceed 2^31 – 1.
Breadth First Search Travering the Binary Tree
If we use the BFS (Breadth First Search) algorithm to traverse the binary tree, we get a level-by-level order. At each node, we need to store the current value from the root to the current node. Also, if the current node is a leaf node, we need to add it to the sum.
When we enqueue the child nodes, we can compute the value by multiple the current value and plus the value for the children nodes. The following C++ code implements the BFS algorithm to sum up the values from the root to the leaf nodes.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ class Solution { public: int sumRootToLeaf(TreeNode* root) { int sum = 0; queue<pair<TreeNode*, int>> q; if (root == NULL) return 0; q.push(make_pair(root, root->val)); // push the root while (q.size() > 0) { auto p = q.front(); q.pop(); TreeNode* node = p.first; int cur = p.second; if (node->left == NULL && node->right == NULL) { // leaf node sum += cur; } else { if (node->left != NULL) { // push left children q.push(make_pair(node->left, cur * 2 + node->left->val)); } if (node->right != NULL) { // push right children q.push(make_pair(node->right, cur * 2 + node->right->val)); } } } return sum; } }; |
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int sumRootToLeaf(TreeNode* root) {
int sum = 0;
queue<pair<TreeNode*, int>> q;
if (root == NULL) return 0;
q.push(make_pair(root, root->val)); // push the root
while (q.size() > 0) {
auto p = q.front();
q.pop();
TreeNode* node = p.first;
int cur = p.second;
if (node->left == NULL && node->right == NULL) { // leaf node
sum += cur;
} else {
if (node->left != NULL) { // push left children
q.push(make_pair(node->left, cur * 2 + node->left->val));
}
if (node->right != NULL) { // push right children
q.push(make_pair(node->right, cur * 2 + node->right->val));
}
}
}
return sum;
}
};When the Binary tree is a singly-directional linked list, the space and time complexity is both O(N). On best cases, the depth of the binary tree is O(logN). The following is a Java equivalent implementation where we use javafx.util.Pair and as you can see, the Java code is quite verbose.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | import javafx.util.Pair; /** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ class Solution { public int sumRootToLeaf(TreeNode root) { int sum = 0; if (root == null) return 0; Queue<Pair<TreeNode, Integer>> q = new LinkedList<Pair<TreeNode, Integer>>(); q.add(new Pair(root, root.val)); while (!q.isEmpty()) { Pair<TreeNode, Integer> p = q.poll(); // pop and return the node from the queue TreeNode node = p.getKey(); int cur = p.getValue(); if (node.left == null && node.right == null) { // sum up the from root to current leaf node sum += cur; } else { if (node.left != null) { // enqueue the left child q.add(new Pair(node.left, cur * 2 + node.left.val)); } if (node.right != null) { // enqueue the right child q.add(new Pair(node.right, cur * 2 + node.right.val)); } } } return sum; } } |
import javafx.util.Pair;
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int sumRootToLeaf(TreeNode root) {
int sum = 0;
if (root == null) return 0;
Queue<Pair<TreeNode, Integer>> q = new LinkedList<Pair<TreeNode, Integer>>();
q.add(new Pair(root, root.val));
while (!q.isEmpty()) {
Pair<TreeNode, Integer> p = q.poll(); // pop and return the node from the queue
TreeNode node = p.getKey();
int cur = p.getValue();
if (node.left == null && node.right == null) { // sum up the from root to current leaf node
sum += cur;
} else {
if (node.left != null) { // enqueue the left child
q.add(new Pair(node.left, cur * 2 + node.left.val));
}
if (node.right != null) { // enqueue the right child
q.add(new Pair(node.right, cur * 2 + node.right.val));
}
}
}
return sum;
}
}Other root to leaves sum:
- Teaching Kids Programming – Depth First Search Algorithm to Sum the Root to Leaf Numbers in Binary Tree
- How to Sum the Root To Leaf in Binary Numbers in a Binary Tree using Breadth First Search?
- Teaching Kids Programming – Breadth First Search Algorithm to Sum Root to Leaf Numbers in Binary Tree
- GoLang: Sum of Root To Leaf Binary Numbers via Depth First Search Algorithm
–EOF (The Ultimate Computing & Technology Blog) —
loading...
Last Post: C++ Algorithm to Remove Outermost Parentheses
Next Post: The Image Smoother Algorithm in C++/Java