P versus NP problem (NP Complete, NP Hard)

P, NP, NP Hard and NP Complete

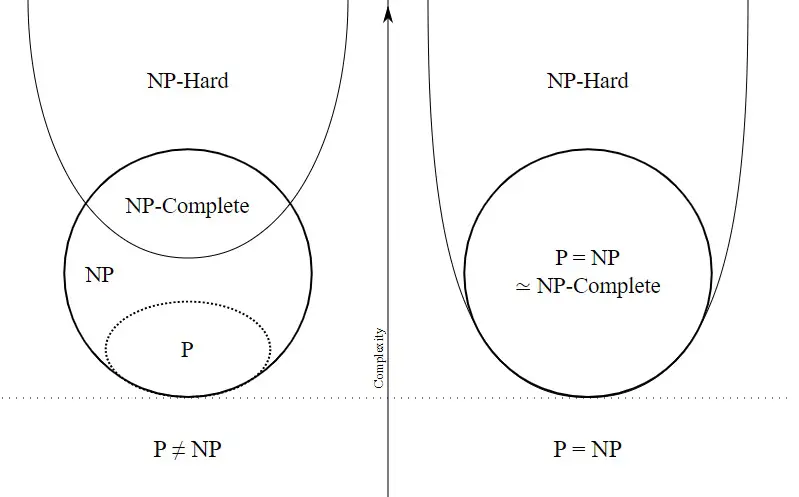
P, NP, NP-hard, and NP-complete are key concepts in computational complexity theory, which helps us classify problems based on how hard they are to solve. Here’s a breakdown:

P (Polynomial Time)

P represents the class of problems that can be solved efficiently by a deterministic algorithm, meaning they can be solved in polynomial time relative to the size of the input. In simple terms, these problems can be solved relatively quickly (e.g., sorting a list or finding the shortest path in a graph). The time required to solve a P problem grows at a polynomial rate (e.g., proportional to O(n^2), O(N^3) etc), where n is the size of the input.

NP (Nondeterministic Polynomial Time)

NP is the class of problems where, given a solution, you can verify its correctness in polynomial time, but it’s not necessarily known whether you can solve it efficiently. In other words, while it may take a long time to find a solution, once you have it, checking if it’s correct is quick. An example is the Traveling Salesman Problem (TSP): finding the shortest route may take a long time, but checking if a given route is the shortest is much faster.

NP-Complete Problems

NP-complete problems are a subset of NP problems that are the “hardest” problems in NP. If you can solve an NP-complete problem in polynomial time, you can solve all NP problems in polynomial time. These problems are both in NP (you can verify a solution in polynomial time) and as hard as any problem in NP (any NP problem can be transformed into an NP-complete problem).

Some classic NP-complete problems are:

• SAT (Boolean satisfiability problem): Given a Boolean formula, can the variables be set in a way that makes the formula true?
• Hamiltonian Path: Is there a path in a graph that visits every vertex exactly once?

NP-Hard Problems

NP-hard problems are at least as hard as NP-complete problems, but they don’t necessarily belong to NP. In other words, they might not have a solution that can be verified in polynomial time, or they could be even harder. NP-hard problems might be optimization problems (e.g., trying to minimize or maximize something), where verifying a given solution is more complicated. If you could solve an NP-hard problem in polynomial time, then you could also solve all NP problems in polynomial time, but NP-hard problems aren’t necessarily in NP.

The P vs. NP Question

One of the biggest unsolved questions in computer science is: Is P equal to NP? If P = NP, it would mean that all problems whose solutions can be verified quickly can also be solved quickly. This would revolutionize computing, but no one has proven this is true or false yet.

If a algorithm time complexity is O(N!), O(2^N).. is it P or NP?

An algorithm with a time complexity of O(N!) or O(2^N) is not considered a P (polynomial-time) algorithm. Here’s why:

Problems in the P class can be solved in polynomial time, which means their time complexity is some polynomial function of the input size, like O(N), O(N^2) etc. These grow relatively slowly compared to non-polynomial functions.

Both O(N!) (factorial time) and O(2^N) (exponential time) grow much faster than any polynomial function. O(N!) grows extremely fast, with N! being the factorial of the input size N. O(2^N) is exponential growth, which also becomes infeasible to compute very quickly as N increases.

Since these complexities grow much faster than any polynomial function, an algorithm with these time complexities is not in P.

Is It NP?

To determine if such an algorithm belongs to NP, it’s important to clarify that NP doesn’t refer to how long it takes to solve a problem, but rather how quickly a solution can be verified once given.

If a problem can be solved with a time complexity of O(N!) or O(2^N), it may or may not be in NP, depending on whether a solution can be verified in polynomial time. If verifying the solution takes polynomial time, then the problem could still belong to the NP class, even though it’s very hard to solve.

O(N!) or O(2^N) is not in P, because the time required to solve the problem grows too fast to be considered “efficient.” Whether it is in NP depends on whether solutions can be verified in polynomial time. If the verification process is polynomial, the problem is in NP, but it’s not guaranteed that every O(N!) or O(2^N) problem is in NP.

Summary of P/NP problems

• P: Problems that can be solved in polynomial time (efficiently).
• NP: Problems whose solutions can be verified in polynomial time.
• NP-complete: The hardest problems in NP; solving one efficiently would solve all NP problems efficiently.
• NP-hard: At least as hard as NP-complete problems; may not even have verifiable solutions in polynomial time.
• These classifications help us understand which problems are computationally feasible and which are likely intractable.

–EOF (The Ultimate Computing & Technology Blog) —