Teaching Kids Programming – Best Time to Buy and Sell Stock (Buy and Sell Once – Three Algorithms)

Teaching Kids Programming: Videos on Data Structures and Algorithms

You are given an array prices where prices[i] is the price of a given stock on the ith day. You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.

Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return 0.

Example 1:
Input: prices = [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.

Example 2:
Input: prices = [7,6,4,3,1]
Output: 0
Explanation: In this case, no transactions are done and the max profit = 0.

Best Time to Buy and Sell Stock via Bruteforce Algorithm

We can bruteforce the day to Buy and Sell the stock. This takes O(N^2) time.

1
2
3
4
5
6
7
8

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        n = len(prices)
        ans = 0
        for i in range(n):
            for j in range(i + 1, n):
                ans = max(ans, prices[j] - prices[i])
        return ans     

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        n = len(prices)
        ans = 0
        for i in range(n):
            for j in range(i + 1, n):
                ans = max(ans, prices[j] - prices[i])
        return ans     

One Pass Linear Algorithm to Track the Lowest

A better approach is to remember the lowest price that we have seen and compute the profit if sold on the day.

1
2
3
4
5
6
7
8

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        low = math.inf
        ans = 0
        for i in prices:
            low = min(low, i)
            ans = max(i - low, ans)
        return ans

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        low = math.inf
        ans = 0
        for i in prices:
            low = min(low, i)
            ans = max(i - low, ans)
        return ans

Time complexity is O(N) and we are using O(1) constant space.

Transformed to Maximum Subarray Sum and then Apply Kadane’s Algorithm

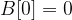Given the prices array and the B array is the difference array, where and 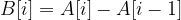if i not equal to zero.

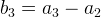
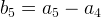
If the lowest point is at a2, and the highest point after a2 is at a5, the max profit we can get is 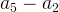, which is the same as 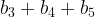i.e. we need to find the maximum sum of subarray – and we can use Kadane’s algorithm.

1
2
3
4
5
6
7

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        ans = cur = 0
        for i in range(1, len(prices)):
            cur = max(0, cur + prices[i] - prices[i - 1])
            ans = max(ans, cur)
        return ans

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        ans = cur = 0
        for i in range(1, len(prices)):
            cur = max(0, cur + prices[i] - prices[i - 1])
            ans = max(ans, cur)
        return ans

Linear time complexity O(N) as we need to go through the array once. And we need a constant time space O(1).

Buy and Sell Stock Algorithms

• C/C++ Coding Exercise – Best Time to Buy and Sell Stock
• Greedy Algorithm Example – What is the Best Time to Buy and Sell Stock?
• Teaching Kids Programming – Best Time to Buy and Sell Stock (Buy and Sell Once – Three Algorithms)

–EOF (The Ultimate Computing & Technology Blog) —