Teaching Kids Programming: Videos on Data Structures and Algorithms
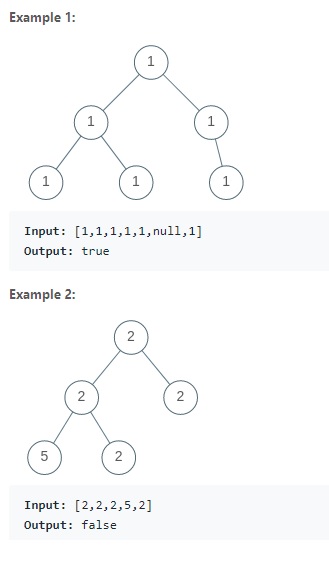
Given a binary tree root, return whether all values in the tree are the same.
Constraints
n ≤ 100,000 where n is the number of nodes in root
Determine a Univalue Binary Tree via Breadth First Search Algorithm
The Breadth First Search Algorithm traverses the binary tree level by level. We then add all the numbers we have met into a hash set, once it contains more than 1 unique numbers, we failed the validation immediately.
Otherwise, we return true when there is none in the queue to proceed i.e. the standard Breadth First Search implementation via a queue.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | # class Tree: # def __init__(self, val, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def isUnivalueBinaryTree(self, root): if not root: return True q = deque([root]) data = set() while len(q) > 0: p = q.popleft() data.add(p.val) if len(data) > 1: return False if p.left: q.append(p.left) if p.right: q.append(p.right) return True |
# class Tree:
# def __init__(self, val, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isUnivalueBinaryTree(self, root):
if not root:
return True
q = deque([root])
data = set()
while len(q) > 0:
p = q.popleft()
data.add(p.val)
if len(data) > 1:
return False
if p.left:
q.append(p.left)
if p.right:
q.append(p.right)
return TrueThe time complexity is O(N), as there are N nodes in the binary tree. The space complexity is O(N) as we are using a queue to implement the BFS, and the set will only be counted as O(1) as we will exit as long as there is more than 1 distinct numbers in the set.
We can remove the early exit check and only check after we finish the traverse:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | # class Tree: # def __init__(self, val, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def solve(self, root): if not root: return True q = deque([root]) data = set() while len(q) > 0: p = q.popleft() data.add(p.val) if p.left: q.append(p.left) if p.right: q.append(p.right) return len(data) == 1 |
# class Tree:
# def __init__(self, val, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def solve(self, root):
if not root:
return True
q = deque([root])
data = set()
while len(q) > 0:
p = q.popleft()
data.add(p.val)
if p.left:
q.append(p.left)
if p.right:
q.append(p.right)
return len(data) == 1See also: How to Count Univalue Subtrees in a Binary Tree?
We can solve this problem using the Depth First Search Algorithm: Teaching Kids Programming – Depth First Search Algorithms to Determine a Univalue Binary Tree
–EOF (The Ultimate Computing & Technology Blog) —
a WordPress rating system
Last Post: Algorithm to Find the Longest Anagram Subsequence
Next Post: Rolling Hash Algorithm to Find the Longest Prefix that Is a Suffix