Teaching Kids Programming – Breadth First Search Algorithm to Find the Sum of Deepest Leaves in a Binary Tree

Teaching Kids Programming: Videos on Data Structures and Algorithms

Given the root of a binary tree, return the sum of values of its deepest leaves.

binary-tree

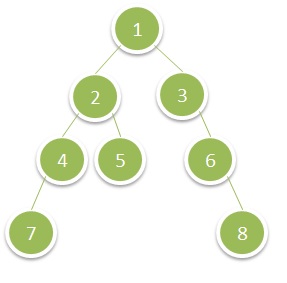
Example 1:
Input: root = [1,2,3,4,5,null,6,7,null,null,null,null,8]
Output: 15

Example 2:
Input: root = [6,7,8,2,7,1,3,9,null,1,4,null,null,null,5]
Output: 19

Constraints:
The number of nodes in the tree is in the range [1, 104].
1 <= Node.val <= 100

Hints:
Traverse the tree to find the max depth.
Traverse the tree again to compute the sum required.

Breadth First Search Algorithm to Find the Sum of Deepest Leaves in a Binary Tree

We can traverse the Binary Tree using Breadth First Search Algorithm. We deque all the nodes (which belong to same level) and then enqueue all their children nodes. At the same time, we compute the sum of these nodes of the same level. When BFS terminates, the sum will be deepest sum.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def deepestLeavesSum(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0        
        q = deque([root])
        ans = 0
        while q:
            n = len(q)
            ans = 0
            for _ in range(n):
                cur = q.popleft()
                if cur.left:
                    q.append(cur.left)
                if cur.right:
                    q.append(cur.right)
                ans += cur.val
        return ans

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def deepestLeavesSum(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0        
        q = deque([root])
        ans = 0
        while q:
            n = len(q)
            ans = 0
            for _ in range(n):
                cur = q.popleft()
                if cur.left:
                    q.append(cur.left)
                if cur.right:
                    q.append(cur.right)
                ans += cur.val
        return ans

Time/Space complexity is O(N) where N is the number of the nodes in the given binary tree. And we are using a queue.

See also: Teaching Kids Programming – Recursive Depth First Search Algorithm to Find the Sum of Deepest Leaves in a Binary Tree

–EOF (The Ultimate Computing & Technology Blog) —