Teaching Kids Programming – Build Progressive Stairs Row by Row via Simulation, Binary Search or Math Algorithm

Teaching Kids Programming: Videos on Data Structures and Algorithms

Given N Coins, we want to build stairs rows by rows, and fill each stair with coin. The first row of stair, there is one coin, the second row 2 coins, and so on. Find out how many complete rows of stairs we can build.

Simulation/Math Algorithm to Build Progressive Stairs

We know the sum for the first N natural integers:

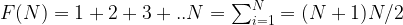
Then, we can start simulation process by filling the coins on the stairs row by row – if we have enough coins for the current row.

1
2
3
4
5
6
7
8
9
10

class Solution:
    def arrangeCoins(self, n: int) -> int:
        assert n >= 0
        rows = 0
        cur = 1
        while n >= cur:
            rows += 1
            n -= cur
            cur += 1
        return rows

class Solution:
    def arrangeCoins(self, n: int) -> int:
        assert n >= 0
        rows = 0
        cur = 1
        while n >= cur:
            rows += 1
            n -= cur
            cur += 1
        return rows

The time complexity is O(M) where M is the iterations for N to be decremented to zero. That is:

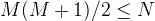
and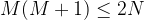
and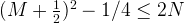
and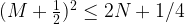
and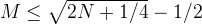

That is,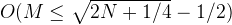

We can actually directly compute the floor value of M that gives us O(1) time.

1
2
3
4

class Solution:
    def arrangeCoins(self, n: int) -> int:
        assert n >= 0
        return floor((2 * n + 0.25)**0.5 - 0.5)

class Solution:
    def arrangeCoins(self, n: int) -> int:
        assert n >= 0
        return floor((2 * n + 0.25)**0.5 - 0.5)

Binary Search Algorithm to Build Progressive Stairs

We can binary search to find the value of M. We can search from [1, N], and compute the actual value of coins required.

1
2
3
4
5
6
7
8
9
10
11
12
13
14

class Solution:
    def arrangeCoins(self, n: int) -> int:
        assert n >= 0
        left, right = 1, n
        while left <= right:
            mid = left + right >> 1
            k = mid * (mid + 1) // 2
            if k == n:
                return mid
            if k < n:   # we have coins left
                left = mid + 1
            else:  # we don't have enough coins
                right = mid - 1
        return left - 1

class Solution:
    def arrangeCoins(self, n: int) -> int:
        assert n >= 0
        left, right = 1, n
        while left <= right:
            mid = left + right >> 1
            k = mid * (mid + 1) // 2
            if k == n:
                return mid
            if k < n:   # we have coins left
                left = mid + 1
            else:  # we don't have enough coins
                right = mid - 1
        return left - 1

The Binary Search algorithm takes O(LogN) time.

–EOF (The Ultimate Computing & Technology Blog) —