Teaching Kids Programming – Closest Binary Search Tree Value (Iterative and Recursive Inorder Traversal Algorithm)

Teaching Kids Programming: Videos on Data Structures and Algorithms

Given the root of a binary search tree and a target value, return the value in the BST that is closest to the target. If there are multiple answers, print the smallest.

A Binary Search Tree

Example 1:
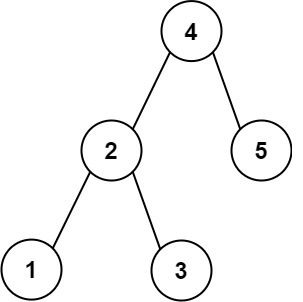
Input: root = [4,2,5,1,3], target = 3.714286
Output: 4

Example 2:
Input: root = [1], target = 4.428571
Output: 1

Constraints:
The number of nodes in the tree is in the range [1, 104].
0 <= Node.val <= 10^9
-10^9 <= target <= 10^9

Closest Binary Search Tree Value (Recursive Inorder Traversal Algorithm)

This is a problem that involves finding the closest value in a binary search tree to a given target value. Before diving into the solution, let’s first understand the problem statement.

Problem Statement

Given the root of a binary search tree and a target value, find the value in the tree that is closest to the target.

Solution Approach

To solve this problem, we can use the inorder traversal of the binary search tree. In an inorder traversal, we visit the left subtree, then the root node, and then the right subtree.

We can use a generator function inorder (Recursion) to implement the inorder traversal of the binary search tree. The inorder function takes a root node as input and yields the values of the nodes in the binary search tree in increasing order.

1
2
3
4
5
6

def inorder(root):
    if not root:
        return
    yield from inorder(root.left)
    yield root.val
    yield from inorder(root.right)

def inorder(root):
    if not root:
        return
    yield from inorder(root.left)
    yield root.val
    yield from inorder(root.right)

We can then create an iterator a that generates the values of the binary search tree in increasing order using the inorder function.

1

a = iter(inorder(root))

a = iter(inorder(root))

We can then iterate through the iterator a and compare the values of the binary search tree with the target value to find the closest value. We use a variable prev to keep track of the previous value in the binary search tree that we have seen.

1
2
3
4
5
6
7
8

prev = -inf
while True:
    x = next(a, None)
    if x is None:
        break
    if prev <= target and target <= x:
        return min(prev, x, key = lambda y: abs(target - y))
    prev = x

prev = -inf
while True:
    x = next(a, None)
    if x is None:
        break
    if prev <= target and target <= x:
        return min(prev, x, key = lambda y: abs(target - y))
    prev = x

If the target value is between the previous value prev and the current value x, then we can return the value that is closest to the target value using the min function and the abs function.

If we have traversed the entire binary search tree and have not found a value that is between the previous value prev and the current value x, then we can return the previous value prev, which is the closest value to the target value.

1

return prev

return prev

Conclusion

This involves finding the closest value in a binary search tree to a given target value. We can use the inorder traversal of the binary search tree and iterate through the values of the binary search tree to find the closest value to the target value. The solution involves creating a generator function to implement the inorder traversal and then using an iterator to generate the values of the binary search tree in increasing order. We then iterate through the iterator and compare the values of the binary search tree with the target value to find the closest value.

The overall solution for this approach – recursive inorder algorithm and stop once we have stepped between the previous and current node in the sorted sequence.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def closestValue(self, root: Optional[TreeNode], target: float) -> int:
        def inorder(root):
            if not root:
                return
            yield from inorder(root.left)
            yield root.val
            yield from inorder(root.right)
 
        a = iter(inorder(root))
        prev = -inf
        while True:
            x = next(a, None)
            if x is None:
                break
            if prev <= target and target <= x:
                return min(prev, x, key = lambda y: abs(target - y))
            prev = x
        return prev

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def closestValue(self, root: Optional[TreeNode], target: float) -> int:
        def inorder(root):
            if not root:
                return
            yield from inorder(root.left)
            yield root.val
            yield from inorder(root.right)

        a = iter(inorder(root))
        prev = -inf
        while True:
            x = next(a, None)
            if x is None:
                break
            if prev <= target and target <= x:
                return min(prev, x, key = lambda y: abs(target - y))
            prev = x
        return prev

The time complexity is O(K) where K is that the node is K-th largest. The space complexity is O(N) due to recursion.

Closest Binary Search Tree Value (Iterative Inorder Traversal Algorithm)

This solution also uses the binary search property of the binary search tree. However, instead of using the inorder traversal, this solution uses a stack to traverse the binary search tree in a slightly different manner.

We start by initializing a variable prev to negative infinity, which will keep track of the closest value we have seen so far.

1

prev = -inf

prev = -inf

We also create an empty stack st to keep track of the nodes we have visited.

1

st = []

st = []

We then use a while loop to iterate through the binary search tree. We continue the loop as long as there are still nodes in the stack or the root node is not None.

1

while st or root:

while st or root:

Inside the loop, we traverse the left subtree of the root node and push all the nodes onto the stack.

1
2
3

while root:
    st.append(root)
    root = root.left

while root:
    st.append(root)
    root = root.left

We then pop the top node from the stack and check if the target value is between the previous value prev and the current value root.val. If it is, we return the value that is closest to the target value using the min function and the abs function.

1
2
3

root = st.pop()
if prev <= target <= root.val:
    return min(prev, root.val, key=lambda x: abs(x - target))

root = st.pop()
if prev <= target <= root.val:
    return min(prev, root.val, key=lambda x: abs(x - target))

If the target value is not between the previous value prev and the current value root.val, we update the previous value prev to the current value root.val and continue to traverse the right subtree of the root node.

1
2

prev = root.val
root = root.right

prev = root.val
root = root.right

If we have traversed the entire binary search tree and have not found a value that is between the previous value prev and the current value root.val, then we can return the previous value prev, which is the closest value to the target value.

1

return prev

return prev

Conclusion

In conclusion, This is a problem that involves finding the closest value in a binary search tree to a given target value. This solution uses a stack to traverse the binary search tree in a slightly different manner. The solution involves initializing a variable prev to negative infinity, creating an empty stack st to keep track of the nodes we have visited, and using a while loop to iterate through the binary search tree. We then check if the target value is between the previous value prev and the current value root.val. If it is, we return the value that is closest to the target value using the min function and the abs function. If the target value is not between the previous value prev and the current value root.val, we update the previous value prev to the current value root.val and continue to traverse the right subtree of the root node. If we have traversed the entire binary search tree and have not found a value that is between the previous value prev and the current value root.val, then we can return the previous value prev, which is the closest value to the target value.

The complete solution is given below:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def closestValue(self, root: Optional[TreeNode], target: float) -> int:
        prev = -inf
        st = []
        while st or root:
            while root:
                st.append(root)
                root = root.left            
            root = st.pop()
            if prev <= target <= root.val:
                return min(prev, root.val, key=lambda x: abs(x - target))
            prev = root.val
            root = root.right
        return prev

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def closestValue(self, root: Optional[TreeNode], target: float) -> int:
        prev = -inf
        st = []
        while st or root:
            while root:
                st.append(root)
                root = root.left            
            root = st.pop()
            if prev <= target <= root.val:
                return min(prev, root.val, key=lambda x: abs(x - target))
            prev = root.val
            root = root.right
        return prev

The time complexity is O(K) if we take K steps to locate the closest node in the given Binary Search Tree. The space complexity is O(N) due to usage of a stack.

Closest Binary Search Tree Value

Finding the Closest Node in a Given Binary Tree can be solved using the following algorithms:

• Teaching Kids Programming – Closest Binary Search Tree Value (Recursion + Inorder Traversal + Binary Search Algorithm)
• Teaching Kids Programming – Closest Binary Search Tree Value (Iterative and Recursive Inorder Traversal Algorithm)

–EOF (The Ultimate Computing & Technology Blog) —