Teaching Kids Programming: Videos on Data Structures and Algorithms
Given a grid with n*m squares (m horizontal squares and n vertical squares), and suppose you are at the top-left square (noted X), count the number of ways to get to the bottom-right corner (noted T) square if you can only walk 1 step east or south a a time.
------- |X| | | ------- | | | | ------- | | |T| -------
Counting via Combination Math
In all, you have to walk n-1 steps south and m-1 steps east. Therefore, there are n+m-2 steps, and you can pick n-1 or m-1 for south or east. That is 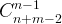 or
or 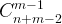
Counting via Dynamic Programming Algorithm
If we use F(n, m) to denote the ways from (0, 0) to go to (n, m), we know it can only comes from (n-1, m) and (n, m-1) thus we can simply add these two:
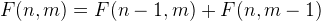
The first column and first row should all be filled with 1 as there is only 1 way from the start:
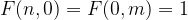
Implemented via Recursion with Memoization (the Top-Down Dynamic Programming Algorithm):
1 2 3 4 5 6 7 8 | def f(n, m, nb = {}): if n == 0 or m == 0: return 1 if (n, m) in nb: return nb[(n, m)] val = f(n-1, m) + f(n, m-1) nb[(n, m)] = val return val |
def f(n, m, nb = {}):
if n == 0 or m == 0:
return 1
if (n, m) in nb:
return nb[(n, m)]
val = f(n-1, m) + f(n, m-1)
nb[(n, m)] = val
return valOr simply, by using the lru_cache to simplify the implementation of Memoization:
1 2 3 4 5 | @lru_cache(None): def f(n, m): if n == 0 or m == 0: return 1 return f(n-1, m) + f(n, m-1) |
@lru_cache(None):
def f(n, m):
if n == 0 or m == 0:
return 1
return f(n-1, m) + f(n, m-1)We can also implement the same algorithm via Bottom-Up Dynamic Programming (starting from the Top-Left corner):
1 2 3 4 5 6 7 8 9 10 11 | def f(n, m): dp = [[0 for _ in range(m)] for _ in range(n)] dp[0][0] = 1 for r in range(n): dp[r][0] = 1 for c in range(m): dp[0][c] = 1 for r in range(1, n): for c in range(1, m): dp[r][c] = dp[r][c - 1] + dp[r - 1][c] return dp[-1][-1] |
def f(n, m):
dp = [[0 for _ in range(m)] for _ in range(n)]
dp[0][0] = 1
for r in range(n):
dp[r][0] = 1
for c in range(m):
dp[0][c] = 1
for r in range(1, n):
for c in range(1, m):
dp[r][c] = dp[r][c - 1] + dp[r - 1][c]
return dp[-1][-1]If we have to visit a intermediate point e.g. (a, b) then the paths can be separated from two parts: (0, 0) to (a, b) and (a, b) to T. Let’s say the first part has A ways and the second part has B ways. There are hence A*B ways all together.
Algorithms to Walk in a Grid
Here are some posts on the path counting or probability on a Grid:
- Teaching Kids Programming – Probability Matrix of Walking in a Grid (Unique Paths)
- Teaching Kids Programming – Count Number of Ways to Walk in a Grid using Dynamic Programming or Combination
- How Many Ways from A to C via B?
–EOF (The Ultimate Computing & Technology Blog) —
loading...
Last Post: Consecutive Ones Algorithm
Next Post: Compute Longest Substring with At Least K Repeating Characters via Divide and Conquer Algorithm