Teaching Kids Programming – Count Servers that Communicate (Hash Map – Counter)

Teaching Kids Programming: Videos on Data Structures and Algorithms

You are given a map of a server center, represented as a m * n integer matrix grid, where 1 means that on that cell there is a server and 0 means that it is no server. Two servers are said to communicate if they are on the same row or on the same column.

Return the number of servers that communicate with any other server.

Count Servers That Communicate

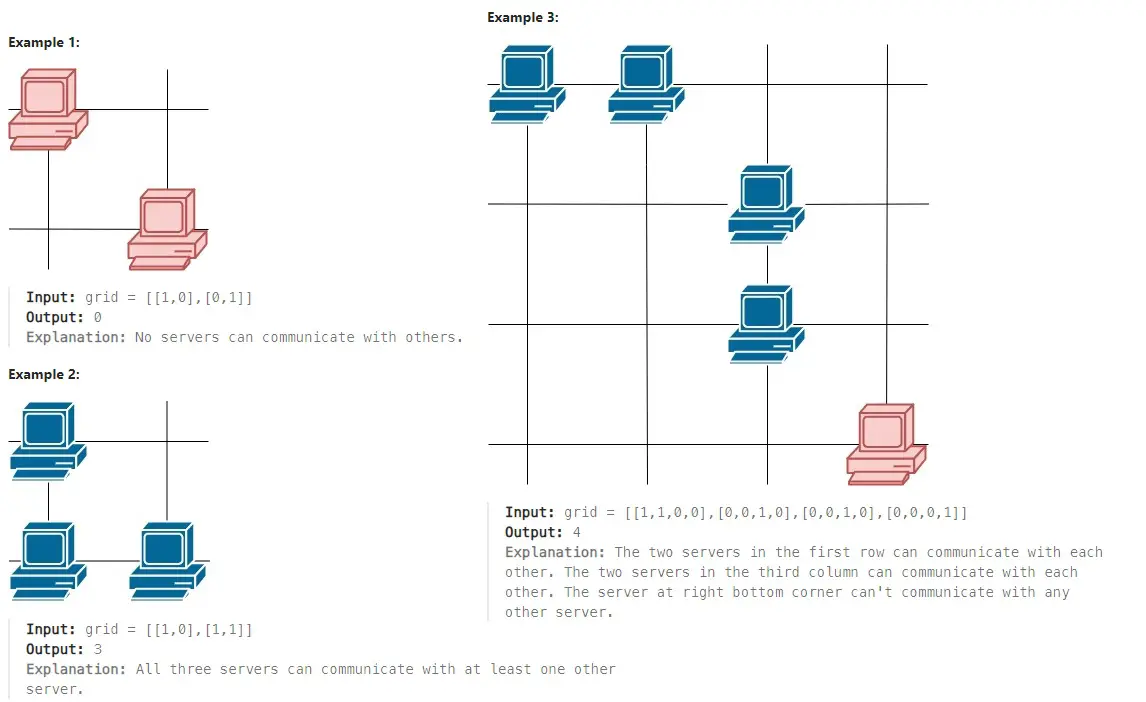
Example 1:
Input: grid = [[1,0],[0,1]]
Output: 0
Explanation: No servers can communicate with others.

Example 2:
Input: grid = [[1,0],[1,1]]
Output: 3
Explanation: All three servers can communicate with at least one other server.

Example 3:
Input: grid = [[1,1,0,0],[0,0,1,0],[0,0,1,0],[0,0,0,1]]
Output: 4
Explanation: The two servers in the first row can communicate with each other. The two servers in the third column can communicate with each other. The server at right bottom corner can’t communicate with any other server.

Constraints:
m == grid.length
n == grid[i].length
1 <= m <= 250
1 <= n <= 250
grid[i][j] == 0 or 1

Count Servers that Communicate (Hash Map – Counter)

We can use two counters (aks Hash Maps) to count the number of servers for each row and column respectively, which requires the first pass to iterate over the grid.

And then a second pass is to count those servers who has at least a neighbour (row counter or column counter is at least two).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

class Solution:
    def countServers(self, grid: List[List[int]]) -> int:
        rc = Counter()
        cc = Counter()
        rows = len(grid)
        cols = len(grid[0])
 
        for r in range(rows):
            for c in range(cols):
                if grid[r][c]:
                    rc[r] += 1
                    cc[c] += 1
 
        ans = 0
        for r in range(rows):
            for c in range(cols):
                if grid[r][c] and (rc[r] > 1 or cc[c] > 1):
                    ans += 1
 
        return ans

class Solution:
    def countServers(self, grid: List[List[int]]) -> int:
        rc = Counter()
        cc = Counter()
        rows = len(grid)
        cols = len(grid[0])

        for r in range(rows):
            for c in range(cols):
                if grid[r][c]:
                    rc[r] += 1
                    cc[c] += 1

        ans = 0
        for r in range(rows):
            for c in range(cols):
                if grid[r][c] and (rc[r] > 1 or cc[c] > 1):
                    ans += 1

        return ans

The time complexity is O(RC) where R and C are the dimensions for the rows and columns respectively. The space complexity is O(R+C) as we are using two hash maps.

–EOF (The Ultimate Computing & Technology Blog) —