Teaching Kids Programming: Videos on Data Structures and Algorithms
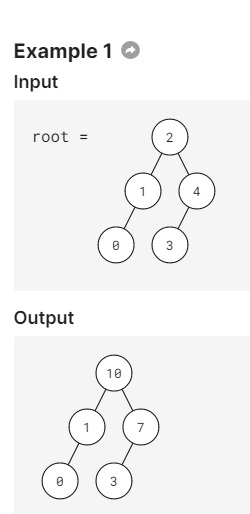
Given a binary tree root, return the same tree except every node’s value is replaced by its original value plus all of the sums of its left and right subtrees.
Constraints
n ≤ 100,000 where n is the number of nodes in root
Depth First Search Algorithm to Convert to Elephant Binary Tree
Basically we want to replace each node with the sum of the subtree. We know the DFS algorithm to compute the sum of a binary tree:
1 2 3 4 5 6 7 | def dfs(root): if not root: return 0 ans = root.val ans += dfs(root.left) ans += dfs(root.right) return ans |
def dfs(root):
if not root:
return 0
ans = root.val
ans += dfs(root.left)
ans += dfs(root.right)
return ansAll we need to do is to change the root’s value to the current sum – and recursively this should convert the binary tree to its elephant version:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | # class Tree: # def __init__(self, val, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def convertToElephantTree(self, root): def dfs(node): if not node: return 0 val = node.val val += dfs(node.left) val += dfs(node.right) # replace with sum of the subtree node.val = val return val dfs(root) return root |
# class Tree:
# def __init__(self, val, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def convertToElephantTree(self, root):
def dfs(node):
if not node:
return 0
val = node.val
val += dfs(node.left)
val += dfs(node.right)
# replace with sum of the subtree
node.val = val
return val
dfs(root)
return rootThe time complexity is O(N) where N is the number of the nodes in the binary tree. The space complexity is O(N) as we are using Recursion which implicitly implies stack.
–EOF (The Ultimate Computing & Technology Blog) —
loading...
Last Post: Using BASH script to Copy Files/Folders to Multiple Remote Servers
Next Post: Using sys_getloadavg and num_cpus in PHP to Throttle API