Teaching Kids Programming – Disjoint Set: Find if Path Exists in Graph via Union Find Algorithm

Teaching Kids Programming: Videos on Data Structures and Algorithms

There is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n – 1 (inclusive). The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [ui, vi] denotes a bi-directional edge between vertex ui and vertex vi. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.

You want to determine if there is a valid path that exists from vertex start to vertex end.

Given edges and the integers n, start, and end, return true if there is a valid path from start to end, or false otherwise.

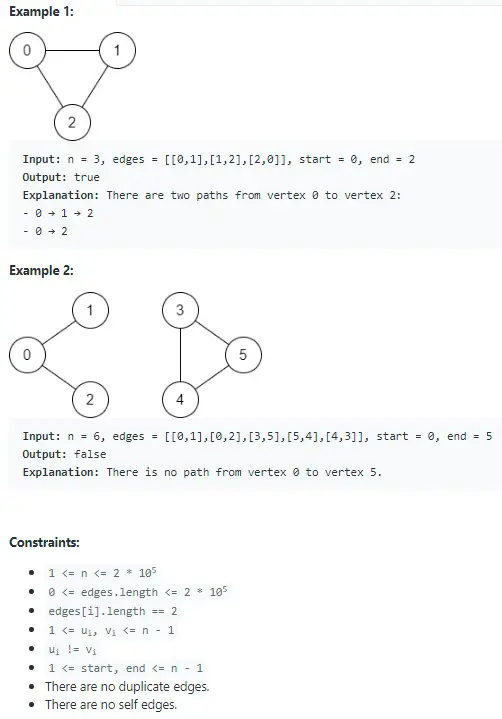
Example 1:
Input: n = 3, edges = [[0,1],[1,2],[2,0]], start = 0, end = 2
Output: true
Explanation: There are two paths from vertex 0 to vertex 2:
– 0 → 1 → 2
– 0 → 2
Example 2:

Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], start = 0, end = 5
Output: false
Explanation: There is no path from vertex 0 to vertex 5.

There are no duplicate edges.
There are no self edges.

Data Structure: Disjoint Set

Union Find Algorithm is based on Disjoint Set where we merge two components and find out if any two belong to same groups. For detailed tutorial on disjoint set – here is a tutorial on the Union Find + Disjoint Set.

To find a parent (root) of a node (and compress the path along the way), we can do this recursively:

1
2
3
4
5
6

def findset(self, x: int) -> int:
    if self.parent[x] == x:
        return x
    # compress the path
    self.parent[x] = self.findset(self.parent[x])
    return self.parent[x]

def findset(self, x: int) -> int:
    if self.parent[x] == x:
        return x
    # compress the path
    self.parent[x] = self.findset(self.parent[x])
    return self.parent[x]

Or, iteratively:

1
2
3
4
5
6
7
8
9
10
11

def findset(self, x: int) -> int:
    px = x
    # find the root
    while px != self.parent[px]:
        px = self.parent[px]
    while x != px:
        i = self.parent[x]
        # compress the path
        self.parent[x] = px
        x = i
    return px

def findset(self, x: int) -> int:
    px = x
    # find the root
    while px != self.parent[px]:
        px = self.parent[px]
    while x != px:
        i = self.parent[x]
        # compress the path
        self.parent[x] = px
        x = i
    return px

And we prefer merging the group of smaller size into a bigger one in order to minimize the total path length:

1
2
3
4
5
6
7
8
9
10
11

def unite(self, x: int, y: int) -> bool:
    x, y = self.findset(x), self.findset(y)
    if x == y:
        return False
    if self.size[x] < self.size[y]:
        x, y = y, x
    # group x is larger than group y
    self.parent[y] = x
    self.size[x] += self.size[y]
    self.setCount -= 1
    return True

def unite(self, x: int, y: int) -> bool:
    x, y = self.findset(x), self.findset(y)
    if x == y:
        return False
    if self.size[x] < self.size[y]:
        x, y = y, x
    # group x is larger than group y
    self.parent[y] = x
    self.size[x] += self.size[y]
    self.setCount -= 1
    return True

The complete class source code for a Disjoint Set can be found at github.

The worst case of finding parent is O(N) if path is not compressed. However, after path compression, the time complexity is O(1) constant.

Find if a Path Exists in Graph using Union Find Algorithm

Given a Graph with N vertices, we just need to create a disjoint set with N groups, then merge the vertices if there is an edge between them.

1
2
3
4
5
6

class Solution:
    def validPath(self, n: int, edges: List[List[int]], start: int, end: int) -> bool:
        UF = UnionFind(n)
        for s, e in edges:
            UF.unite(s, e)
        return UF.connected(start, end)            

class Solution:
    def validPath(self, n: int, edges: List[List[int]], start: int, end: int) -> bool:
        UF = UnionFind(n)
        for s, e in edges:
            UF.unite(s, e)
        return UF.connected(start, end)            

A path exists between v1 to v2 if vertex v1 and v2 belong to the same group.

We can always solve the problem via DFS and BFS.

Path Finding between two vertices in a Graph:

• Teaching Kids Programming – Find if Path Exists in Graph via Depth First Search Algorithm
• Teaching Kids Programming – Find if Path Exists in Graph via Breadth First Search Algorithm
• Teaching Kids Programming – Disjoint Set: Find if Path Exists in Graph via Union Find Algorithm

–EOF (The Ultimate Computing & Technology Blog) —