Teaching Kids Programming – Introduction to Heap and Priority Queue

Teaching Kids Programming: Videos on Data Structures and Algorithms

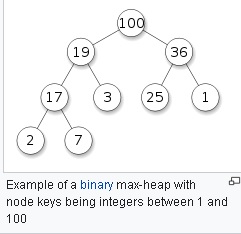
A Heap is a tree data structure the root of which is the smallest (min heap) or the largest (max heap). The heap tree has to be complete. For example, in a binary heap, the binary tree is a complete binary tree where each level has to contain all nodes except the last level (leaves) which may not be complete.

The leaf nodes have to be on the left as much as possible. A perfect binary heap tree is also a complete binary heap tree where all level of nodes including the leaf nodes are all present.

A priority queue is a First In Priority Out (ADT = Advance Data Type). We push the elements to a priority queue (just like normal queue First In First Out), however, when an element is popped, the priority queue will choose a highest priority (by default, the minimal element in Python) to dequeue.

A priority queue can be implemented as a heap data structure.

heapq module in Python

In Python, we can use the heapq module, we can do this:

1

import heapq as hq

import heapq as hq

heapify to turn into a heap

The “hp” is the alias for the heapq module, then we can use the heapify to turn a list/array into a heap:

1
2

data = [3, 2, 1]
hq.heapify(data) # data is now [1, 2, 3]

data = [3, 2, 1]
hq.heapify(data) # data is now [1, 2, 3]

Building a heap with N elements takes O(N) time.

heappush to push an element to the heap/priority queue

we can use the heappush to insert an element into the priority queue/heap. The time complexity is O(LogN) to rebuild the heap.

1
2
3
4

data = [3, 2, 1]
hq.heapify(data) # data is now [1, 2, 3]
hq.heappush(data, 4)
hq.heapify(data) # data is now [1, 2, 3, 4]

data = [3, 2, 1]
hq.heapify(data) # data is now [1, 2, 3]
hq.heappush(data, 4)
hq.heapify(data) # data is now [1, 2, 3, 4]

heappop to remove an element from the heap/priority queue

To deque, we use the heappop which takes also the O(LogN) to rebuild the heap / priority queue.

1
2
3

data = [3, 2, 1]
hq.heapify(data) # data is now [1, 2, 3]
x = hq.heappop(data) # data is now [2, 3] and x is 1

data = [3, 2, 1]
hq.heapify(data) # data is now [1, 2, 3]
x = hq.heappop(data) # data is now [2, 3] and x is 1

Maximum Heap in Python

Before pushing to heap, we can multiply the elements by -1 so that the smallest becomes the largest, and vice versa. This way, we can use the heapq as a max heap.

1
2
3
4
5
6
7
8
9

import heapq as hq
 
data = []
for i in [3, 5, 2]:
    hq.heappush(data, -i)
 
while len(data) > 0:
    x = hq.heappop(data)
    print(-x)

import heapq as hq

data = []
for i in [3, 5, 2]:
    hq.heappush(data, -i)

while len(data) > 0:
    x = hq.heappop(data)
    print(-x)

nlargest and nsmallest

We can use the nlargest and nsmallest to obtain the N largest or smallest elements from the heap/priority queue

1
2
3
4
5
6

data = [1, 5, 2, 3, 7, 6, 8]
hq.heapify(data)
smallest = hq.nsmallest(3, data) # [1, 2, 3]
print(data) # [1, 3, 2, 5, 7, 6, 8]
largest = hq.nlargest(2, data) # [8, 7]
print(data) # [1, 3, 2, 5, 7, 6, 8]

data = [1, 5, 2, 3, 7, 6, 8]
hq.heapify(data)
smallest = hq.nsmallest(3, data) # [1, 2, 3]
print(data) # [1, 3, 2, 5, 7, 6, 8]
largest = hq.nlargest(2, data) # [8, 7]
print(data) # [1, 3, 2, 5, 7, 6, 8]

As you can see, the nlargest and nsmallest won’t modify (deque) the heap.

heappushpop and heapreplace

heappushpop is equivalent as first heappush and then heappop but slightly faster and heapreplace is same as first heappop and then heappush (but slightly faster).

1
2
3
4
5
6
7
8

import heapq as hq
 
data = [3, 2, 5, 1, 4]
hq.heapify(data)
x = hq.heappushpop(data, 6)
print(x, data) # 1 [2, 3, 5, 6, 4]
y = hq.heapreplace(data, 7)
print(y, data) # 2 [3, 4, 5, 6, 7]

import heapq as hq

data = [3, 2, 5, 1, 4]
hq.heapify(data)
x = hq.heappushpop(data, 6)
print(x, data) # 1 [2, 3, 5, 6, 4]
y = hq.heapreplace(data, 7)
print(y, data) # 2 [3, 4, 5, 6, 7]

–EOF (The Ultimate Computing & Technology Blog)