Teaching Kids Programming – Last Moment Before All Ants Fall Out of a Plank

Teaching Kids Programming: Videos on Data Structures and Algorithms

We have a wooden plank of the length n units. Some ants are walking on the plank, each ant moves with a speed of 1 unit per second. Some of the ants move to the left, the other move to the right.

When two ants moving in two different directions meet at some point, they change their directions and continue moving again. Assume changing directions does not take any additional time.

When an ant reaches one end of the plank at a time t, it falls out of the plank immediately.

Given an integer n and two integer arrays left and right, the positions of the ants moving to the left and the right, return the moment when the last ant(s) fall out of the plank.

Leetcode 1503. Last Moment Before All Ants Fall Out of a Plank

Example 1:
Input: n = 4, left = [4,3], right = [0,1]
Output: 4
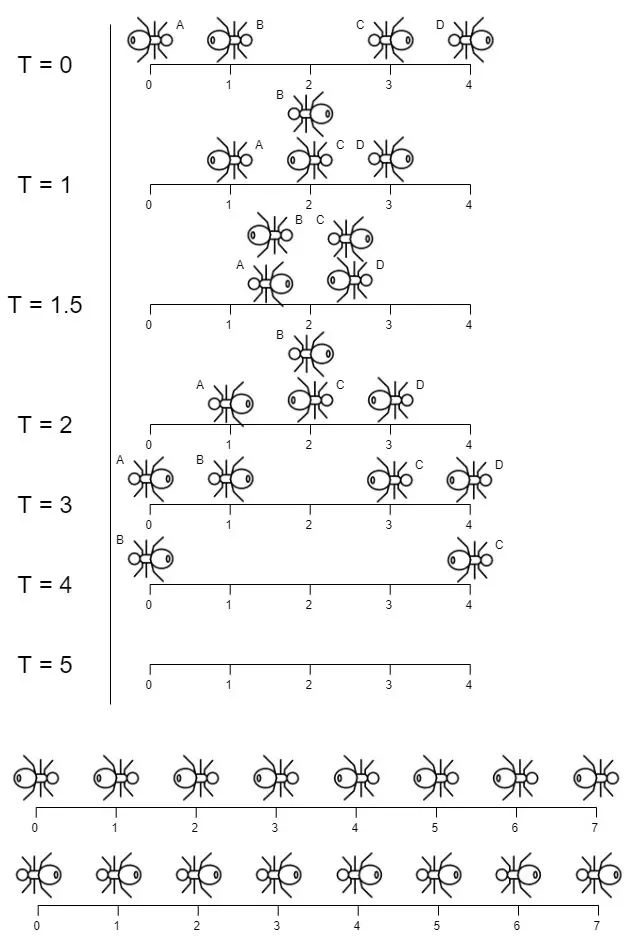
Explanation: In the image above:
-The ant at index 0 is named A and going to the right.
-The ant at index 1 is named B and going to the right.
-The ant at index 3 is named C and going to the left.
-The ant at index 4 is named D and going to the left.
The last moment when an ant was on the plank is t = 4 seconds. After that, it falls immediately out of the plank. (i.e., We can say that at t = 4.0000000001, there are no ants on the plank).

Example 2:
Input: n = 7, left = [], right = [0,1,2,3,4,5,6,7]
Output: 7
Explanation: All ants are going to the right, the ant at index 0 needs 7 seconds to fall.

Example 3:
Input: n = 7, left = [0,1,2,3,4,5,6,7], right = []
Output: 7
Explanation: All ants are going to the left, the ant at index 7 needs 7 seconds to fall.

Constraints:
1 <= n <= 10^4
0 <= left.length <= n + 1
0 <= left[i] <= n
0 <= right.length <= n + 1
0 <= right[i] <= n
1 <= left.length + right.length <= n + 1
All values of left and right are unique, and each value can appear only in one of the two arrays.

Last Moment Before All Ants Fall Out of a Plank

When two ants meet each other, they change to opposite direction with zero delay. This is same as the ants pass by each other without affecting the overall result. All the ants are same size, same speed, so when they hit each other, it is Elastic Collision. The speed is the same, and the direction is opposite after collision.

We can then find the last moment for all the ants facing left and right respectively. The last moment is the ant which is far from the end: smallest value for right-facing, and largest value for left-facing. The time complexity is O(L+R). The space complexity is O(1).

1
2
3
4
5
6
7
8

class Solution:
    def getLastMoment(self, n: int, left: List[int], right: List[int]) -> int:
        ans = 0
        for i in left:
            ans = max(ans, i)
        for i in right:
            ans = max(ans, n - i)
        return ans

class Solution:
    def getLastMoment(self, n: int, left: List[int], right: List[int]) -> int:
        ans = 0
        for i in left:
            ans = max(ans, i)
        for i in right:
            ans = max(ans, n - i)
        return ans

The implementation can be simplified using one-liner. The default parameter is required to deal with the cases when input array is empty.

1
2
3

class Solution:
    def getLastMoment(self, n: int, left: List[int], right: List[int]) -> int:
        return max(max(left, default=0), max((n - i for i in right), default=0))

class Solution:
    def getLastMoment(self, n: int, left: List[int], right: List[int]) -> int:
        return max(max(left, default=0), max((n - i for i in right), default=0))

–EOF (The Ultimate Computing & Technology Blog) —