Teaching Kids Programming – 0/1 Knapsack: Length of the Longest Subsequence That Sums to Target (Recursion+Memoization=Top Down Dynamic Programming)

Teaching Kids Programming: Videos on Data Structures and Algorithms

You are given a 0-indexed array of integers nums, and an integer target. Return the length of the longest subsequence of nums that sums up to target. If no such subsequence exists, return -1. A subsequence is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.

Example 1:
Input: nums = [1,2,3,4,5], target = 9
Output: 3
Explanation: There are 3 subsequences with a sum equal to 9: [4,5], [1,3,5], and [2,3,4]. The longest subsequences are [1,3,5], and [2,3,4]. Hence, the answer is 3.

Example 2:
Input: nums = [4,1,3,2,1,5], target = 7
Output: 4
Explanation: There are 5 subsequences with a sum equal to 7: [4,3], [4,1,2], [4,2,1], [1,1,5], and [1,3,2,1]. The longest subsequence is [1,3,2,1]. Hence, the answer is 4.

Example 3:
Input: nums = [1,1,5,4,5], target = 3
Output: -1
Explanation: It can be shown that nums has no subsequence that sums up to 3.

Constraints:
1 <= nums.length <= 1000
1 <= nums[i] <= 1000
1 <= target <= 1000

Hint 1
Use dynamic programming.
Hint 2
Let dp[i][j] be the maximum length of any subsequence of nums[0..i – 1] that sums to j.
Hint 3
dp[0][0] = 1, and dp[0][j] = 1 for all target ≥ j > 0.
Hint 4
dp[i][j] = max(dp[i – 1][j], dp[i – 1][j – nums[i -1]) for all n ≥ i > 0 and target ≥ j > nums[i – 1].

Length of the Longest Subsequence That Sums to Target (Recursion+Memoization=Top Down Dynamic Programming)

We have seen similar problems before regarding the Longest Subsequence, for instance, the length of the Longest Increasing Subsequence.

This is a kind of knapsack problem where we aim to maximize the number of the items put in the knapsack given that the total weights of the items equal to a target. Each item can be put or skip, so this is a 0/1 Knapsack problem.

0/1 Knapsack Problem: Longest Subsequence That Sums to Target

Given: 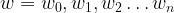which is the weights for each item
That: 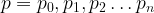where 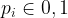i.e. when 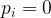it means we don’t want to pick the item i, and when 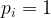it means that we pick the item i.
We want to maximize the sum of the picks aka.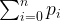
Subject to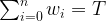

Solving the Longest Subsequence That Sums to Target via Recursion and Memoization which is Top Down Dynamic Programming

For each item, we can pick or skip, so we can solve this via Recursion, and with the @cache aka the memoization, we literally make it a Top Down Dynamic Programming Algorithm.

We cache/remember all the stats which is L*S where L is the length of the array, and S is the number of unique sums.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution:
    def lengthOfLongestSubsequence(self, nums: List[int], target: int) -> int:
        ## optionally sorting the array to make it practically faster.
        nums.sort(reverse=True)
 
        @cache
        def f(i, x):
            ## if we run out of the numbers
            if i == len(nums):
                return 0 if x == 0 else -inf
            ## if the sum exceeds
            if x < 0:
                return -inf
            ## to pick            
            a = f(i + 1, x - nums[i])
            if a != -inf:
                a += 1
            ## to skip
            b = f(i + 1, x)
            return max(a, b)
 
        ans = f(0, target)
        ## to clear the cache betweeen different tests runs.
        f.cache_clear()
        return ans if ans != -inf else -1

class Solution:
    def lengthOfLongestSubsequence(self, nums: List[int], target: int) -> int:
        ## optionally sorting the array to make it practically faster.
        nums.sort(reverse=True)

        @cache
        def f(i, x):
            ## if we run out of the numbers
            if i == len(nums):
                return 0 if x == 0 else -inf
            ## if the sum exceeds
            if x < 0:
                return -inf
            ## to pick            
            a = f(i + 1, x - nums[i])
            if a != -inf:
                a += 1
            ## to skip
            b = f(i + 1, x)
            return max(a, b)

        ans = f(0, target)
        ## to clear the cache betweeen different tests runs.
        f.cache_clear()
        return ans if ans != -inf else -1

The time/space complexity is O(LS), and we can sort the numbers in the descending order to make it a bit faster in practice.

Knapsack Problems

• Teaching Kids Programming - 0/1 Knapsack: Length of the Longest Subsequence That Sums to Target (Recursion+Memoization=Top Down Dynamic Programming)
• Teaching Kids Programming - 0/1 Knapsack Space Optimised Dynamic Programming Algorithm
• Teaching Kids Programming - Using Bottom Up Dynamic Programming Algorithm to Solve 0/1 Knapsack Problem
• Teaching Kids Programming - 0/1 Knapsack Problem via Top Down Dynamic Programming Algorithm
• Teaching Kids Programming - Multiple Strange Coin Flips/Toss Bottom Up Dynamic Programming Algorithm (Knapsack Variant)
• Teaching Kids Programming - Multiple Strange Coin Flips/Toss Top Down Dynamic Programming Algorithm (Knapsack Variant)
• Teaching Kids Programming - Max Profit of Rod Cutting (Unbounded Knapsack) via Bottom Up Dynamic Programming Algorithm
• Teaching Kids Programming - Max Profit of Rod Cutting (Unbounded Knapsack) via Top Down Dynamic Programming Algorithm
• Teaching Kids Programming - Brick Layout (Unlimited Knapsack) via Bottom Up Dynamic Programming Algorithm
• Teaching Kids Programming - Brick Layout (Unlimited Knapsack) via Top Down Dynamic Programming Algorithm
• Count Multiset Sum (Knapsacks) by Dynamic Programming Algorithm
• Count Multiset Sum (Knapsacks) by Recursive BackTracking Algorithm
• Dynamic Programming Algorithm to Solve the Poly Knapsack (Ubounded) Problem
• Dynamic Programming Algorithm to Solve 0-1 Knapsack Problem
• Classic Unlimited Knapsack Problem Variant: Coin Change via Dynamic Programming and Depth First Search Algorithm
• Classic Knapsack Problem Variant: Coin Change via Dynamic Programming and Breadth First Search Algorithm
• Complete Knapsack Problem
• 0/1 Knapsack Problem
• Teaching Kids Programming - Combination Sum Up to Target (Unique Numbers) by Dynamic Programming Algorithms
• Algorithms Series: 0/1 BackPack - Dynamic Programming and BackTracking
• Using BackTracking Algorithm to Find the Combination Integer Sum
• Facing Heads Probabilties of Tossing Strange Coins using Dynamic Programming Algorithm
• Partition Equal Subset Sum Algorithms using DFS, Top-Down and Bottom-up DP

–EOF (The Ultimate Computing & Technology Blog) —