Teaching Kids Programming – Longest Increasing Subsequence via Dynamic Programming Algorithm

Teaching Kids Programming: Videos on Data Structures and Algorithms

Given an integer array nums, return the length of the longest strictly increasing subsequence. A subsequence is a sequence that can be derived from an array by deleting some or no elements without changing the order of the remaining elements. For example, [3,6,2,7] is a subsequence of the array [0,3,1,6,2,2,7].

Example 1:
Input: nums = [10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.

Example 2:
Input: nums = [0,1,0,3,2,3]
Output: 4

Example 3:
Input: nums = [7,7,7,7,7,7,7]
Output: 1

Bruteforcing takes O(2^N) to enumerate all subsequences and then we need O(N) time to check each subsequence, which amounts up to complexity O(N*2^N) which is not feasible to solve using the modern computers.

Bottom-Up Dynamic Programming Algorithm to Find the Longest Increasing Subsequence

We can use the Dynamic Programming Algorithm to Solve this problem in O(N^2) quadratic time. Let F(N) be the number of the longest subsequence that ends nums[N], and the DP relation equation is:

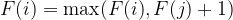where j is smaller than i and nums[j] is smaller than nums[i].
Initialize F(i) to 1 where i is [1, N].

The Bottom-up Dynamic Programming Algorithm to Find the Longest Increasing Subsequence in Python is implemented as following:

1
2
3
4
5
6
7
8
9
10
11

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if not nums:
            return 0
        n = len(nums)
        dp = [1] * (n + 1)
        for i in range(n):
            for j in range(i + 1, n):
                if nums[j] > nums[i]:
                    dp[j] = max(dp[j], dp[i] + 1)
        return max(dp)

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if not nums:
            return 0
        n = len(nums)
        dp = [1] * (n + 1)
        for i in range(n):
            for j in range(i + 1, n):
                if nums[j] > nums[i]:
                    dp[j] = max(dp[j], dp[i] + 1)
        return max(dp)

We use a DP array and thus the space complexity is O(N).

Finding the Longest Increasing Subsequence via Top-Down Dynamic Programming Algorithm

We can do this via Recursion + Memoization aka Top-Down Dynamic Programming Algorithm. To compute F(N) value, we need to check the values between nums[0] to nums[N-1] and if it is smaller than nums[N], we recursively calling F function with a smaller value. But we have to use @cache (or @lru_cache(None), or @lru_cache(maxsize=None)) to rememebr the values that we already know so that we don’t re-calculate them over and over agin.

1
2
3
4
5
6
7
8
9
10
11
12

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if not nums:
            return 0
        @cache
        def f(i):
            ans = 1
            for j in range(i):
                if nums[j] < nums[i]:
                    ans = max(ans, f(j) + 1)
            return ans            
        return max(f(i) for i in range(len(nums)))

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if not nums:
            return 0
        @cache
        def f(i):
            ans = 1
            for j in range(i):
                if nums[j] < nums[i]:
                    ans = max(ans, f(j) + 1)
            return ans            
        return max(f(i) for i in range(len(nums)))

Time complexity is still O(N^2) quadratic and the space complexity is O(N).

Longest Increasing SubSequence

• Teaching Kids Programming – Longest Increasing Subsequence via Dynamic Programming Algorithm
• How to Find the Length of the Longest Increasing Subsequence using Dynamic Programming Algorithm?
• Teaching Kids Programming – Greedy Algorithm to Find Longest Increasing Subsequence in O(NLogN) via Binary Search

–EOF (The Ultimate Computing & Technology Blog) —