Teaching Kids Programming – Longest Strictly Increasing Then Decreasing Sublist

Teaching Kids Programming: Videos on Data Structures and Algorithms

You are given a list of integers nums. Return the length of the longest sublist such that its length is at least 3 and its values are strictly increasing and then decreasing. Both the increasing part and the decreasing part must be non-empty.

Constraints
n ≤ 100,000 where n is the length of nums
Example 1
Input
nums = [7, 1, 3, 5, 2, 0]
Output
5
Explanation
The sublist [1, 3, 5, 2, 0] is strictly increasing then decreasing.

Example 2
Input
nums = [1, 2, 3]
Output
0

Example 3
Input
nums = [3, 2, 1]
Output
0

Example 4
Input
nums = [1, 2, 1, 1]
Output
3

Hints:
Can you break the problem into finding the longest increasing and longest decreasing sublists?
keep 2 auxiliary arrays to keep the length of strictly decreasing sublist starting at every point and the length of strictly increasing sublist ending at that every point.
Think about the sublist with increasing and decreasing parts which we can create by considering each index as starting point

Longest Strictly Increasing Then Decreasing Sublist

The bruteforce algorithms would take O(N^3) – as we need O(N^2) to generate all sublists 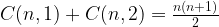. And it takes another O(N) to check if a sublist is increasing and then decreasing. C(n,1) picks 1 out of n – which corresponds to sublist of size 1. C(n,2) picks 2 (indices, e.g i and j) out of n, which corresponds to sublist s[i:j+1].

We can have two arrays: pre-calculating the longest length of sublists that ends or starts at that index for the increasing or decreasing sublists respectively. We can use previous values aka Dynamic Programming Algorithms to calculate the length at that index, we start from left to right for the increasing sublist lengths and we start from right to left for the decreasing sublist lengths.

Then, we can go through the nums again: if both the sublist length at that location is larger than 1, we can add them and minus one (as we count the number at that index twice).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

class Solution:
    def longestIncreasingAndDecreasingSubList(self, nums):
        n = len(nums)
        lis = [1] * n
        lds = [1] * n
        for i in range(1, n):
            if nums[i] > nums[i - 1]:
                lis[i] += lis[i - 1]
        for i in range(n - 2, -1, -1):
            if nums[i] > nums[i + 1]:
                lds[i] += lds[i + 1]
        ans = 0
        for i in range(n):
            a = lis[i]
            b = lds[i]
            if a > 1 and b > 1:
                ans = max(ans, a + b - 1)
        return ans

class Solution:
    def longestIncreasingAndDecreasingSubList(self, nums):
        n = len(nums)
        lis = [1] * n
        lds = [1] * n
        for i in range(1, n):
            if nums[i] > nums[i - 1]:
                lis[i] += lis[i - 1]
        for i in range(n - 2, -1, -1):
            if nums[i] > nums[i + 1]:
                lds[i] += lds[i + 1]
        ans = 0
        for i in range(n):
            a = lis[i]
            b = lds[i]
            if a > 1 and b > 1:
                ans = max(ans, a + b - 1)
        return ans

The time complexity is O(N) – 3 passes of the array. And the space complexity is O(N) as we need two arrays.

–EOF (The Ultimate Computing & Technology Blog) —