Teaching Kids Programming – Permutation of K out of N Visible Blocks via Top Down Dynamic Programming Algorithm

Teaching Kids Programming: Videos on Data Structures and Algorithms

You are given two integers n and k. There are n blocks with heights ranging from 1 to n. Return the number of ways in which these n blocks can be arranged, in such a way that if you look from the left, exactly k blocks are visible.

For example, if n = 5, one way to arrange the blocks is:

                                *
                        *       *
                *       *       *
        *       *       *       * 
*       *       *       *       *
---------------------------------

Constraints
1 ≤ k ≤ n < 15
Example 1
Input
n = 4
k = 2
Output
11
Explanation
We can have the following arrangements in which we can see 2 blocks from the left side:

1 2 3 4 5 6 7 8 9 10 11

[1, 4, 3, 2] [1, 4, 2, 3] [2, 1, 4, 3] [2, 4, 1, 3] [2, 4, 3, 1] [3, 1, 2, 4] [3, 1, 4, 2] [3, 2, 4, 1] [3, 2, 1, 4] [3, 4, 1, 2] [3, 4, 2, 1]

[1, 4, 3, 2]
[1, 4, 2, 3]
[2, 1, 4, 3]
[2, 4, 1, 3]
[2, 4, 3, 1]
[3, 1, 2, 4]
[3, 1, 4, 2]
[3, 2, 4, 1]
[3, 2, 1, 4]
[3, 4, 1, 2]
[3, 4, 2, 1]

solve(n,k) means you have n blocks and you want k blocks to be visible from the left side. Now you have two possibilities for the smallest block available. Either you put the smallest block in the front, or anywhere else.

solve(n,k) means you have n blocks and you want k blocks to be visible from the left side. Now you have two possibilities for the smallest block available. Either you put the smallest block in the front, or anywhere else.

If you put the smallest block on the first position then this will be visible to you and now you only need k-1 more blocks to be visible to in this case you need to call solve(n – 1, k – 1). Otherwise you can choose any of the position other than very front position , so you will have (n-1) positions to choose and wherever you place this block this will not be visible. so you need to call (n – 1) * solve(n-1, k).

If you put the smallest block on the first position then this will be visible to you and now you only need k-1 more blocks to be visible to in this case you need to call solve(n – 1, k – 1). Otherwise you can choose any of the position other than very front position , so you will have (n-1) positions to choose and wherever you place this block this will not be visible. so you need to call (n – 1) * solve(n-1, k).

Together we will need to call solve(n – 1, k – 1) + (n – 1) * solve(n – 1, k). Together we will need to call solve(n – 1, k – 1) + (n – 1) * solve(n – 1, k)

Permutation of K out of N Visible Blocks via Top Down Dynamic Programming Algorithm

Let f(n, k) be the number of ways we can re-order the N blocks so that exactly k blocks are visible from the left side.

When k=n meaning that we must see all blocks, and there could be only one way which is to put the blocks from the smallest to the largest (sorted, 1 to n). In other words, if the blocks are not in order, some blocks will be not seen due to being blocked by some larger blocks on the left.

1
2

if k == n:
    return 1

if k == n:
    return 1

When k=1 meaning that we can only see one block. We must put the largest block on the left, and rest n-1 blocks do not matter how they are put – which could have 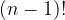aka the factorial, full permutation.

1
2

if k == 1:
    return math.factorial(n - 1)

if k == 1:
    return math.factorial(n - 1)

In other cases, we can put the smallest block on the leftmost, then we have n-1 blocks left and k-1 blocks to be seen. The leftmost block is always visible. If we don’t put the smallest block on the leftmost, we have n-1 places to put, and since it is the smallest, it can’t be seen from the left, then we still have k blocks to “see” and we have n-1 blocks left i.e. f(n-1, k). We need to multiply this with n-1.

1

return f(n - 1, k - 1) + (n - 1) * f(n - 1, k)

return f(n - 1, k - 1) + (n - 1) * f(n - 1, k)

Let’s implement this using Recursion – as we already have the recurrence math formula.

1
2
3
4
5
6
7
8
9

@cache
def f(n, k):
    if n < k:
        return 0
    if k == 1:
        return factorial(n - 1)
    if n == k:
        return 1
    return f(n - 1, k - 1) + (n - 1) * f(n - 1, k)

@cache
def f(n, k):
    if n < k:
        return 0
    if k == 1:
        return factorial(n - 1)
    if n == k:
        return 1
    return f(n - 1, k - 1) + (n - 1) * f(n - 1, k)

We shall return 0 if we have n blocks but want to see k blocks (k is larger than n) – which is common sense. We should cache the intermediate values using memoization technique e.g. adding a @cache or @lru_cache(None) in Python.

The total number of states is n*k, thus the time/space complexity is O(n*k).

–EOF (The Ultimate Computing & Technology Blog) —