Teaching Kids Programming – Reachable Nodes With Restrictions (Graph Theory, Breadth First Search Algorithm, Undirected/Unweighted Graph)

Teaching Kids Programming: Videos on Data Structures and Algorithms

There is an undirected tree with n nodes labeled from 0 to n – 1 and n – 1 edges.

You are given a 2D integer array edges of length n – 1 where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree. You are also given an integer array restricted which represents restricted nodes.

Return the maximum number of nodes you can reach from node 0 without visiting a restricted node.

Note that node 0 will not be a restricted node.

Undirected Unweighted Graph Traversal Algorithms with Restriction

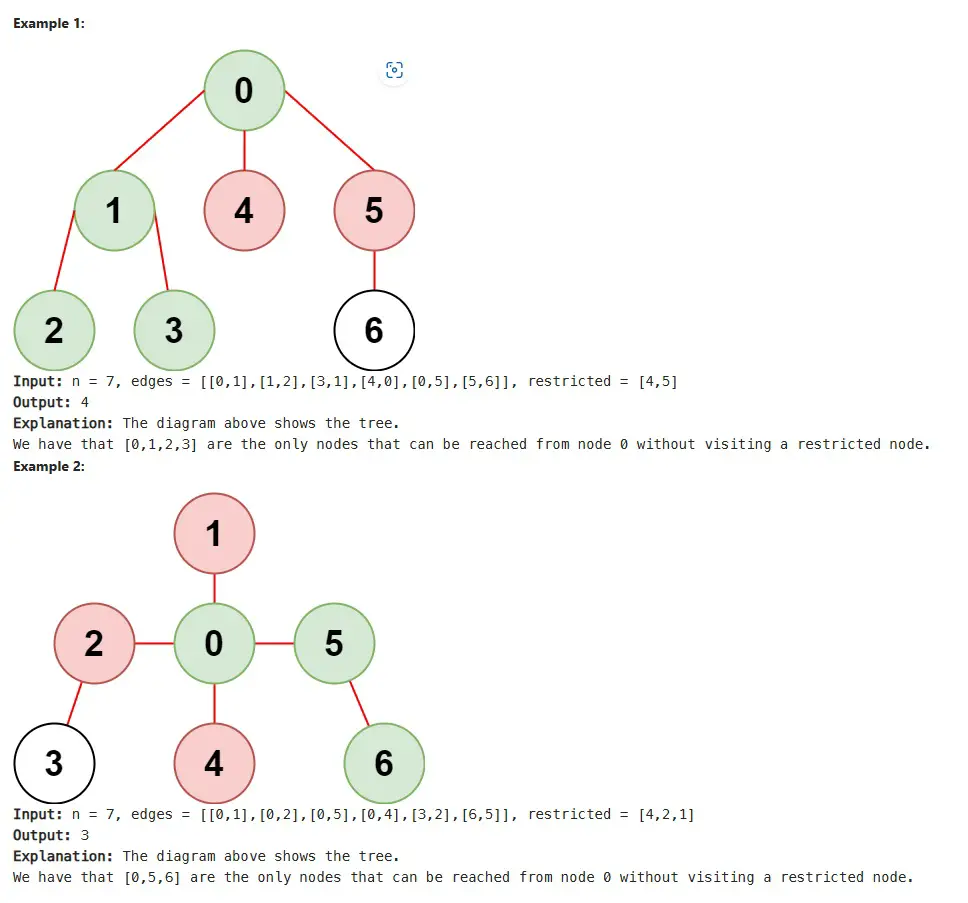
Example 1:
Input: n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
Output: 4
Explanation: The diagram above shows the tree.
We have that [0,1,2,3] are the only nodes that can be reached from node 0 without visiting a restricted node.

Example 2:
Input: n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]
Output: 3
Explanation: The diagram above shows the tree.
We have that [0,5,6] are the only nodes that can be reached from node 0 without visiting a restricted node.

Constraints:
2 <= n <= 10^5
edges.length == n – 1
edges[i].length == 2
0 <= ai, bi < n
ai != bi
edges represents a valid tree.
1 <= restricted.length < n
1 <= restricted[i] < n
All the values of restricted are unique.

Hints:
Can we find all the reachable nodes in a single traversal?
Hint 2
Traverse the graph from node 0 while avoiding the nodes in restricted and do not revisit nodes that have been visited.
Hint 3
Keep count of how many nodes are visited in total.

Reachable Nodes With Restrictions (Graph Theory, Breadth First Search Algorithm)

We can solve this problem by performing a Breadth First Search algorithm from the Node 0. We enqueue the node as long as it is not in forbidden set and also it is not visited before (using Hash Set). The number of the vertices that can be visited is the size of the hash set which contains the nodes/vertices that have connectivity to the starting node 0.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

class Solution:
    def reachableNodes(self, n: int, edges: List[List[int]], restricted: List[int]) -> int:        
        R = set(restricted)
        G = defaultdict(list)
        for a, b in edges:
            G[a].append(b)
            G[b].append(a)
        seen = set([0])
        st = deque([0])
        while st:
            c = st.popleft()
            for x in G[c]:
                if x not in seen and x not in R:
                    seen.add(x)
                    st.append(x)
        return len(seen)

class Solution:
    def reachableNodes(self, n: int, edges: List[List[int]], restricted: List[int]) -> int:        
        R = set(restricted)
        G = defaultdict(list)
        for a, b in edges:
            G[a].append(b)
            G[b].append(a)
        seen = set([0])
        st = deque([0])
        while st:
            c = st.popleft()
            for x in G[c]:
                if x not in seen and x not in R:
                    seen.add(x)
                    st.append(x)
        return len(seen)

We use a double-ended queue to perform the Breadth First Search as push/pop on both sides of the queue is O(1) constant. The order of the Graph traversal does not matter in this problem thus we can also solve this using Depth First Search Algorithm.

Reachable Nodes With Restrictions (Graph Theory)

• Teaching Kids Programming - Reachable Nodes With Restrictions (Graph Theory, Iterative Depth First Search Algorithm, Undirected/Unweighted Graph)
• Teaching Kids Programming - Reachable Nodes With Restrictions (Graph Theory, Union Find, Disjoint Set, Undirected/Unweighted Graph)
• Teaching Kids Programming - Reachable Nodes With Restrictions (Graph Theory, Recursive Depth First Search Algorithm)
• Teaching Kids Programming - Reachable Nodes With Restrictions (Graph Theory, Breadth First Search Algorithm, Undirected/Unweighted Graph)

–EOF (The Ultimate Computing & Technology Blog