Teaching Kids Programming – Uniform Cost Search Algorithm to Solve Single-Source Shortest Path in a Graph

Teaching Kids Programming: Videos on Data Structures and Algorithms

You are given a two-dimensional list of integers edges which represents a directed, weighted graph. Each element in edges contains [u, v, w] meaning that there is an edge from node u to node v which costs positive weight w. You are also given integers start and end.

Return the cost of the shortest path from start to end. If there is no path between the two nodes, return -1.

Constraints
1 ≤ n ≤ 100,000 where n is the length of edges
Example 1
Input

1 2 3 4 5

edges = [     [0, 1, 3],     [1, 2, 2],     [0, 2, 9] ]

edges = [
    [0, 1, 3],
    [1, 2, 2],
    [0, 2, 9]
]

start = 0
end = 2
Output
5
Explanation
We can go 0 to 1 for cost of 3 and then 1 to 2 for cost of 2.

Uniform Cost Search Algorithm

Uniform Cost Search (UCS) is like Breadth First Search (BFS) Algorithm but that can be used on weighted Graphs. UCS uses a priority queue instead of a normal queue.

And at start, it pushes the source into the priority queue (First In, Highest Priority Out) with initial cost zero. Then while the priority queue is not empty, it will pop a highest priority (shortest path, lowest accumulated cost from source) from the priority queue. If the vertex is the destination, great, then end the algorithms and return the cost which is from the source. Otherwise, enqueue all the children of current node to the queue with the corresponding costs.

We also need to maintain a visited set so that we don’t end up in cycles. Uniform Cost Search Algorithm only concerns the path cost rather than the number of the steps involved in searching.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

class Solution:
    def shortestPathUsingUCS(self, edges, s, e):
        G = defaultdict(list[int])
        for a, b, c in edges:
            G[a].append((b, c))
        q = [(0, s)]
        seen = set()
        while q:
            d, cur = heappop(q)
            if cur == e:
                return d
            if cur in seen:
                continue
            seen.add(cur)
            for n, c in G[cur]:
                heappush(q, (d + c, n))
        return -1

class Solution:
    def shortestPathUsingUCS(self, edges, s, e):
        G = defaultdict(list[int])
        for a, b, c in edges:
            G[a].append((b, c))
        q = [(0, s)]
        seen = set()
        while q:
            d, cur = heappop(q)
            if cur == e:
                return d
            if cur in seen:
                continue
            seen.add(cur)
            for n, c in G[cur]:
                heappush(q, (d + c, n))
        return -1

In Python, we can use heappush and heappop from heapq as a priority queue. You can also use the PriorityQueue class for custom comparator. When the costs are all one, the UCS is actually the same as BFS. Compared to Floyd multi-source shortest path algorithm, UCS is a single source shortest path algorithm that is more efficient.

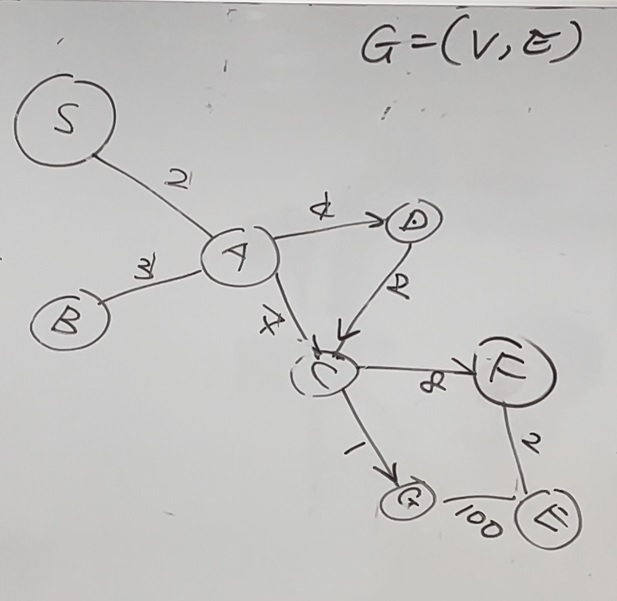
Given this Graph (weighted and directed):

Steps for Uniform Cost Search:

1. Visited={}, Q=[(S,0)]
2. Deque=S, Visited={S}, Q=[(A,2)]
3. Deque=A, Visited={S,A}, Q=[(D,6),(B,5),(C,9)]
4. Deque=B, Visited={S,A,B}, Q=[(D,6),(C,9)]
5. Deque=D, Visited={S,A,B,D}, Q=[(C,9),(C,8)]
6. Deque=C(8), Visited={S,A,B,D,C}, Q=[(C,9),(F,16),(G,9)]
7. Deque=C(9), Visited={S,A,B,D,C}, Q=[(F,16),(G,9)]
8. Deque=G, Visited={S,A,B,D,C,G, Q=[(F,16),(E,109)]
9. Deque=F, Visited={S,A,B,D,C,G,F}, Q=[(G,18),(E,109)]
10. Deque=G,18, as G is the destination, we stop the UCS and return the cumulated cost which is 18

Shortest Path Algorithms

• Teaching Kids Programming – Distance Between Bus Stops (Floyd Warshal Shortest Path in Simple Undirected Weighted Regular Graph)
• Teaching Kids Programming – Depth First/Limit Search and Iterative Deepening Search Algorithm on Unweighted Graph
• Teaching Kids Programming – A Light Talk on Breadth First Search, Uniform Cost Search and Dijkstra Shortest Path Graph Algorithms
• Teaching Kids Programming – Introduction to Dijkstra Single Source Shortest Path Graph Algorithm
• Teaching Kids Programming – Single Source Shortest Path Algorithm in a Directed Unweighted Graph using Breadth First Search
• Teaching Kids Programming – Floyd Warshal Multi-source/All Pairs Shortest Path Algorithm (Sum of Costs in a Directed Unweighted Graph)
• Teaching Kids Programming – Uniform Cost Search Algorithm to Solve Single-Source Shortest Path in a Graph
• Teaching Kids Programming – Shortest Path Algorithms by Iterative Deepening Search (IDS), Depth First Search (DFS) or Breadth First Search (BFS) on Undirected Graphs
• Teaching Kids Programming – Finding the Network Delay Time via Floyd-Warshall Shortest Path Algorithm
• Teaching Kids Programming – Distance Between Bus Stops (Shortest Distance in Simple Undirected Weighted Regular Graph)

–EOF (The Ultimate Computing & Technology Blog) —