In [here], the algorithm is introduced that counts the average number of addition for sum to reach one, which approximates the math constant 
. The following will count the probability using an array (e.g. similar to buckets).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | #!/usr/bin/env python from random import seed, random cnt = [0] * 20 def count(): global cnt x = 0 s = 0 while True: s += random() x += 1 if s >= 1: break cnt[x] += 1 for x in range(0, 100000): count() for x in cnt: print x |
#!/usr/bin/env python
from random import seed, random
cnt = [0] * 20
def count():
global cnt
x = 0
s = 0
while True:
s += random()
x += 1
if s >= 1:
break
cnt[x] += 1
for x in range(0, 100000):
count()
for x in cnt:
print xAs expected, after quite a long term iteration, the appearance of answer two (two numbers adds to a number larger than one) is dominanting.
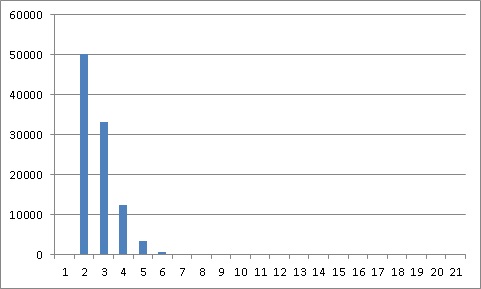
0 0 50106 33285 12402 3412 667 109 18 1 0 0 0 0 0 0 0 0 0 0
The plot is here.
See also: Simple and Efficient C Program to Compute the Mathematic Constant E (Euler’s number)
–EOF (The Ultimate Computing & Technology Blog) —
GD Star Rating
loading...
254 wordsloading...
Last Post: Boy or Girl? Python Validation
Next Post: How Many Zeros at the end of 1024!?