The NegaBinary Algorithm – How to Convert to Base Minus Two (-2) ?

We know the binary conversion, which is base two. The algorithm to convert to binary for a decimal integer, is to divide by two and concatenate the remainder in the reverse order. How about negative base – for example, base minus two – or negabinary?

Given any base r, we can rewrite every integer uniquely as follows:

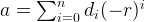
Why Negative Base?

One advantage of using negative base is that we don’t need a sign bit. For positive base like binary, a signed-integer which is 32 bit, however, the left-most bit (most significant bit) is used to represent the sign.

In negabinary, there is no sign bit. For example:

-15 = 110001 because (-2)^0 + (-2)^4 + (-2)^5 = 1 + 16 – 32.

Given a number N, return a string consisting of “0”s and “1”s that represents its value in base -2 (negative two). The returned string must have no leading zeroes, unless the string is “0”.

Example 1:

Input: 2
Output: “110”
Explantion: (-2) ^ 2 + (-2) ^ 1 = 2

Example 2:
Input: 3
Output: “111”
Explantion: (-2) ^ 2 + (-2) ^ 1 + (-2) ^ 0 = 3

Example 3:
Input: 4
Output: “100”
Explantion: (-2) ^ 2 = 4

0 <= N <= 10^9

How to Convert to Base -2 by Adjusting Remainder and Quotient?

The simplistic method is to adjust the remainder and quotient, as followed C++ implementation shows:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

class Solution {
public:
    string baseNeg2(int N) {
        string r = "";
        while (N != 0) {
            int rem = N % (-2);
            N /= (-2);
            if (rem < 0) {
                rem += 2;  // make remainder positive
                N ++;      // adjust the quotient
            }
            r = std::to_string(rem) + r;            
        }        
        return r == "" ? "0" : r;
    }
};

class Solution {
public:
    string baseNeg2(int N) {
        string r = "";
        while (N != 0) {
            int rem = N % (-2);
            N /= (-2);
            if (rem < 0) {
                rem += 2;  // make remainder positive
                N ++;      // adjust the quotient
            }
            r = std::to_string(rem) + r;            
        }        
        return r == "" ? "0" : r;
    }
};

For the proof and how it works, you might refer to the wiki: https://en.wikipedia.org/wiki/Negative_base#Calculation

How to Convert to Base -2 by using Odd/Even rules?

As you might notice, for even bits, the values are the same as it were the positive base: (-2)^4 = (2)^4. When it comes to the odd bits, we might need to manually change the sign:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

class Solution {
public:
    string baseNeg2(int N) {
        string r = "";
        while (N != 0) {
            int rem = N % (-2);
            if (r.size() % 2 == 0) {
                N = (N - rem) / 2;
            } else {
                N = (N + rem) / 2;
            }
            r = std::to_string(rem) + r;            
        }        
        return r == "" ? "0" : r;
    }
};

class Solution {
public:
    string baseNeg2(int N) {
        string r = "";
        while (N != 0) {
            int rem = N % (-2);
            if (r.size() % 2 == 0) {
                N = (N - rem) / 2;
            } else {
                N = (N + rem) / 2;
            }
            r = std::to_string(rem) + r;            
        }        
        return r == "" ? "0" : r;
    }
};

Both algorithms work at O(logN) time and space complexity – if we consider the string concatenation in C++ works O(1). You can always pre-allocate the string buffer or using StringBuilder in Java or C# to make it trivial.

–EOF (The Ultimate Computing & Technology Blog) —