Tower of Hanoi, Recursion

The problem of ‘Tower of Hanoi’ is a very classic problem/puzzle that is often used to teach recursion in Computer Science. The problem can be described as moving a set of disks from one rod to another using a third rod as a temporary one. There are three rods, and all the disks are placed at the first one initially. The sizes of the disks are noted as 1 to n, 1 being the smallest and n being the largest. In any time, a larger disk cannot be on top of a smaller one. And each time, it is only allowed to move one disk.

The problem looks complicated at first but it can be easily solved with recursion, decomposing the case n with a less-complicated situation of (n – 1). We can move the top n – 1 disks (treated as an individual) from rod ‘A’ to ‘B’, and move the disk n (the bottom, the largest disk) from rod ‘A’ to ‘C’, and finally move top n – 1 disks from ‘B’ to ‘C’, in this way, we move n disks from ‘A’ to ‘C’, using ‘B’ as the temporary rod.

Solving Hanoi Tower by Recursion

We can solve this by using Recursion: first move the top N-1 disks and then the N-th disk from A to C – finally move the N-1 disks to C.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

#!/usr/bin/env python
# Hanoi Towers
# https://helloacm.com
 
total = 0
 
def hanoi(n, frm, to, tmp):
    global total
    if n:
        hanoi(n - 1, frm, tmp, to)
        print "Move %d From %s To %s" % (n, frm, to)
        total += 1
        hanoi(n - 1, tmp, to, frm)
 
hanoi(4, 'A', 'C', 'B')
print "total = ", total

#!/usr/bin/env python
# Hanoi Towers
# https://helloacm.com

total = 0

def hanoi(n, frm, to, tmp):
    global total
    if n:
        hanoi(n - 1, frm, tmp, to)
        print "Move %d From %s To %s" % (n, frm, to)
        total += 1
        hanoi(n - 1, tmp, to, frm)

hanoi(4, 'A', 'C', 'B')
print "total = ", total

For four disks on 3 rods, it prints the solution.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

Move 1 From A To B
Move 2 From A To C
Move 1 From B To C
Move 3 From A To B
Move 1 From C To A
Move 2 From C To B
Move 1 From A To B
Move 4 From A To C
Move 1 From B To C
Move 2 From B To A
Move 1 From C To A
Move 3 From B To C
Move 1 From A To B
Move 2 From A To C
Move 1 From B To C
total = 15

Move 1 From A To B
Move 2 From A To C
Move 1 From B To C
Move 3 From A To B
Move 1 From C To A
Move 2 From C To B
Move 1 From A To B
Move 4 From A To C
Move 1 From B To C
Move 2 From B To A
Move 1 From C To A
Move 3 From B To C
Move 1 From A To B
Move 2 From A To C
Move 1 From B To C
total = 15

We notice that the total steps for moving disks is 1, 3, 7, 15, 31 … for the problem size equal to 1, 2, 3, 4, 5 respectively. So we may guess the total number of steps for h(n)is the total number of disks,  is .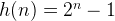

From the above algorithm, we have this recurrence formula: 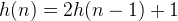, with the terminal condition 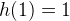. e.g. (move directly from ‘A’ to ‘C’ for one disk). We can prove this by math induction

,

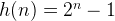One can image moving disks for problem size equal to 64 takes ages, because the total steps is 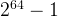one cannot finish moving considering each second moving 1 disk, during his/her entire life.

See Math Induction Proof of the minimal number of moves by Hanoi Tower: Teaching Kids Programming – Tower of Hanoi via Recursion (Math Induction Proof of Minimal Number of Moves)

–EOF (The Ultimate Computing & Technology Blog) —