Breadth First Search Algorithm to Check Completeness of a Binary Tree?

Given a binary tree, determine if it is a complete binary tree.

Definition of a complete binary tree from Wikipedia:
In a complete binary tree every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.

Example 1:

Example of a Complete Binary Tree

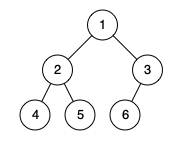
Input: [1,2,3,4,5,6]
Output: true
Explanation: Every level before the last is full (ie. levels with node-values {1} and {2, 3}), and all nodes in the last level ({4, 5, 6}) are as far left as possible.

Example 2:

This Binary Tree is Not Complete

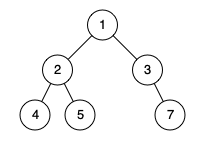
Input: [1,2,3,4,5,null,7]
Output: false
Explanation: The node with value 7 isn’t as far left as possible.

Note:
The tree will have between 1 and 100 nodes.

How to check if a binary tree is complete using BFS algorithm?

We know that the BFS (Breadth First Search) can be used to do level-by-level traversal of a tree (not necessary to be binary), or a graph. And BFS is usually implemented by a queue where we enqueue the children nodes of the front of the queue at each iteration.

We can enqueue the children nodes even if they are null to the queue, and whenever we visit the null node, we know it should not meet other leaves nodes unless all the nodes are traversed.

The following Java code illustrates the BFS algorithm and it runs at O(N) time complexity where the N is the number of nodes of the binary tree. The space complexity is also O(N) where we need to use a queue (or you can replace it with a fixed-size array that implements the circular queue).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isCompleteTree(TreeNode root) {
        if (root == null) return true;
        Queue<TreeNode> q = new LinkedList<TreeNode>();
        q.add(root);
        boolean end = false;
        while (!q.isEmpty()) {
            TreeNode p = q.poll();   // remove the node from the queue
            if (p == null) {
                end = true; 
            } else {
                if (end) return false;  // not complete because we meet other leaves
                q.add(p.left);
                q.add(p.right);
            }
        }
        return true;
    }
}

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isCompleteTree(TreeNode root) {
        if (root == null) return true;
        Queue<TreeNode> q = new LinkedList<TreeNode>();
        q.add(root);
        boolean end = false;
        while (!q.isEmpty()) {
            TreeNode p = q.poll();   // remove the node from the queue
            if (p == null) {
                end = true; 
            } else {
                if (end) return false;  // not complete because we meet other leaves
                q.add(p.left);
                q.add(p.right);
            }
        }
        return true;
    }
}

The following is the C++ code that implements the BFS as well.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isCompleteTree(TreeNode* root) {
        if (root == nullptr) return true;
        queue<TreeNode*> Q;
        Q.push(root);
        bool end = false;
        while (!Q.empty()) {
            auto p = Q.front();
            Q.pop();
            if (p == nullptr) {
                end = true;   // set the flag
            } else {
                if (end) return false; // meet other nodes after null
                Q.push(p->left);
                Q.push(p->right);
            }
        }
        return true;
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isCompleteTree(TreeNode* root) {
        if (root == nullptr) return true;
        queue<TreeNode*> Q;
        Q.push(root);
        bool end = false;
        while (!Q.empty()) {
            auto p = Q.front();
            Q.pop();
            if (p == nullptr) {
                end = true;   // set the flag
            } else {
                if (end) return false; // meet other nodes after null
                Q.push(p->left);
                Q.push(p->right);
            }
        }
        return true;
    }
};

See also: Teaching Kids Programming – Breadth First Search Algorithm to Check the Completeness of a Binary Tree

–EOF (The Ultimate Computing & Technology Blog) —