Home
Compute the Deepest Leaves Sum of a Binary Tree using BFS or DFS Algorithms
Tags:, , , , ,

Compute the Deepest Leaves Sum of a Binary Tree using BFS or DFS Algorithms

December 29, 2019 No Comments algorithms, BFS, c / c++, DFS

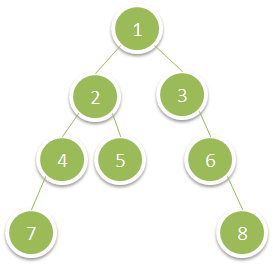
Given a binary tree, return the sum of values of its deepest leaves.

Example 1:
Input: root = [1,2,3,4,5,null,6,7,null,null,null,null,8]
Output: 15

binary-tree Compute the Deepest Leaves Sum of a Binary Tree using BFS or DFS Algorithms algorithms BFS c / c++ DFS

binary-tree

Constraints:
The number of nodes in the tree is between 1 and 10^4.
The value of nodes is between 1 and 100.

We can traversal the binary tree using level-by-level namely Breadth First Search algorithm or depth first search.

Breadth First Search Algorithm to Compute the Deepest Leaves Sum of a Binary Tree

We can expand all the nodes in the same level by sum up on those. However, we need to reset the sum to zero when expanding a new level, then the last sum would be the answer we are looking for.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int deepestLeavesSum(TreeNode* root) {
        if (!root) return 0;
        queue<TreeNode*> Q;
        Q.push(root);
        int sum;
        while (!Q.empty()) {
            sum = 0;  // reset the sum for a new level
            int curSize = Q.size();
            for (int i = 0; i < curSize; ++ i) {
                auto p = Q.front();
                sum += p->val;
                Q.pop();
                if (p->left) {
                    Q.push(p->left);
                }
                if (p->right) {
                    Q.push(p->right);
                }
            }
        }
        return sum;
    }
};
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int deepestLeavesSum(TreeNode* root) {
        if (!root) return 0;
        queue<TreeNode*> Q;
        Q.push(root);
        int sum;
        while (!Q.empty()) {
            sum = 0;  // reset the sum for a new level
            int curSize = Q.size();
            for (int i = 0; i < curSize; ++ i) {
                auto p = Q.front();
                sum += p->val;
                Q.pop();
                if (p->left) {
                    Q.push(p->left);
                }
                if (p->right) {
                    Q.push(p->right);
                }
            }
        }
        return sum;
    }
};

The time complexity is O(N) and the space requirement is also O(N) where N is the number of the nodes in the binary tree.

How to Compute the Deepest Leaves Sum of a Binary Tree using Depth First Search Algorithms

We can store the node values in a hash map either unordered_map or map where the key is the depth and the value is the vector of the values. At the same time, we keep track of the maximum depth we’ve visited.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int deepestLeavesSum(TreeNode* root) {
        helper(root, 0);
        int sum = 0;
        for (const auto &n: data[curMax]) {
            sum += n;
        }
        return sum;
    }
private:
    unordered_map<int, vector<int>> data;
    int curMax = -1;
    void helper(TreeNode* root, int depth) {
        if (root == nullptr) return;        
        curMax = max(curMax, depth);
        data[depth].push_back(root->val);
        helper(root->left, depth + 1);
        helper(root->right, depth + 1);
    }
};
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int deepestLeavesSum(TreeNode* root) {
        helper(root, 0);
        int sum = 0;
        for (const auto &n: data[curMax]) {
            sum += n;
        }
        return sum;
    }
private:
    unordered_map<int, vector<int>> data;
    int curMax = -1;
    void helper(TreeNode* root, int depth) {
        if (root == nullptr) return;        
        curMax = max(curMax, depth);
        data[depth].push_back(root->val);
        helper(root->left, depth + 1);
        helper(root->right, depth + 1);
    }
};

The C++ map sorts the keys by default, meaning that we can use the rbegin() or –end() to get the maximum key for the map. This simplifies the implementation. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int deepestLeavesSum(TreeNode* root) {
        helper(root, 0);
        int sum = 0;
        for (const auto &n: data.rbegin()->second) {
            sum += n;
        }
        return sum;
    }
private:
    map<int, vector<int>> data;
    void helper(TreeNode* root, int depth) {
        if (root == nullptr) return;        
        data[depth].push_back(root->val);
        helper(root->left, depth + 1);
        helper(root->right, depth + 1);
    }
};
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int deepestLeavesSum(TreeNode* root) {
        helper(root, 0);
        int sum = 0;
        for (const auto &n: data.rbegin()->second) {
            sum += n;
        }
        return sum;
    }
private:
    map<int, vector<int>> data;
    void helper(TreeNode* root, int depth) {
        if (root == nullptr) return;        
        data[depth].push_back(root->val);
        helper(root->left, depth + 1);
        helper(root->right, depth + 1);
    }
};

The above DFS implementations have O(N) space requirement (usage of std::map or std::unordered_map), and O(N) time where N is the number of nodes to visit.

Another solution would be to compute the depth of the binary tree first, then compute the sum only for the maximum depth. Both DFS are implemented in Recursion. The sum will be accumulated only when we reach the depth. N nodes will be visited twice.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int deepestLeavesSum(TreeNode* root) {
        if (!root) return 0;
        int depth = getDepth(root);
        return getSumAt(root, depth);
    }
private:
    int getDepth(TreeNode* root) {
        if (root == NULL) return 0;
        return max(getDepth(root->left), getDepth(root->right)) + 1;
    }
    int getSumAt(TreeNode* root, int depth) {
        if (root == NULL) return 0;
        if (depth == 1) return root->val;
        return getSumAt(root->left, depth - 1) + 
            getSumAt(root->right, depth - 1);
    }
};
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int deepestLeavesSum(TreeNode* root) {
        if (!root) return 0;
        int depth = getDepth(root);
        return getSumAt(root, depth);
    }
private:
    int getDepth(TreeNode* root) {
        if (root == NULL) return 0;
        return max(getDepth(root->left), getDepth(root->right)) + 1;
    }
    int getSumAt(TreeNode* root, int depth) {
        if (root == NULL) return 0;
        if (depth == 1) return root->val;
        return getSumAt(root->left, depth - 1) + 
            getSumAt(root->right, depth - 1);
    }
};

See posts of computing the sum of the deepest leaves for a given binary tree:

–EOF (The Ultimate Computing & Technology Blog) —

GD Star Rating
loading...
924 words
Last Post: Microbit Programming: Snake Game with Growing Body and Greedy Strategy
Next Post: Replace Elements with Greatest Element on Right Side using C++ std::exchange() method

The Permanent URL is: Compute the Deepest Leaves Sum of a Binary Tree using BFS or DFS Algorithms

Related posts:

  1. Fixing Profile Query Command due to API Change in Steem Blockchain Due to an API change in SteemIt see this post, the following code to get...
  2. How to Determine Sum of Two Square Numbers? Given a non-negative integer c, your task is to decide whether there’re two integers a...
  3. The Secure Shell (SSH) Chrome Extension developed by Google Speaking about SSH tools, we often use the PuTTY or Termius, which are heavy weight...
  4. Algorithms to Determine a Palindrome Number Determine whether an integer is a palindrome. An integer is a palindrome when it reads...
  5. You need a Numeric Keypad to Start with Your HHKB! Getting a HHKB and being excited for a few days? Sooner or later, you ‘ll...
  6. The Review of cozmo robot from Anki The ANKI COZMO robot is fun – I got it from Amazon and it is...
  7. Find the largest palindrome From the product of two 3-digit numbers A palindromic number reads the same both ways. The largest palindrome made from the product...
  8. How to Compute the Number of Pawns-Captures for Rook in Chess? On an 8 x 8 chessboard, there is one white rook. There also may be...

Leave a Reply