Count Multiset Sum (Knapsacks) by Dynamic Programming Algorithm

Given a list of unique positive integers nums and a positive integer k, return the number of unique combinations that sum up to k. You may reuse numbers when creating combinations.

Constraints
n ≤ 25 where n is the length of nums
1 ≤ nums[i] ≤ 250 for all 0 ≤ i < n 1 ≤ k ≤ 500 Example 1 Input nums = [1, 2, 3] k = 2 Output 2 Explanation We can make 2 with [1, 1] and [2].

Dynamic Programming Algorithm to Count Multiset Sum (Knapsacks)

Given N items which have corresponding weights, and the knapsack capacity is k. Find the number of ways to pack the knapsack full with items. We can do this with Backtracking algorithm where we simulate the packing process: Count Multiset Sum (Knapsacks) by Recursive BackTracking Algorithm

We can also solve this using Dynamic Programming Algorithm. Let dp[i] represent the number of ways to pack with items that sum up to i:

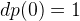
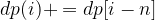where n is the weights

The following time complexity is O(KN) – bottom up Dynamic Programming.

1
2
3
4
5
6
7
8
9
10
11
12

int countMultisetSum(vector<int>& nums, int k) {
    vector<int> dp(k + 1, 0);
    dp[0] = 1;
    for (auto &n: nums) {
        for (int i = 1; i <= k; ++ i) {        
            if (n <= i) {
                dp[i] += dp[i - n];
            }
        }
    }
    return dp.back();
}

int countMultisetSum(vector<int>& nums, int k) {
    vector<int> dp(k + 1, 0);
    dp[0] = 1;
    for (auto &n: nums) {
        for (int i = 1; i <= k; ++ i) {        
            if (n <= i) {
                dp[i] += dp[i - n];
            }
        }
    }
    return dp.back();
}

See also: Dynamic Programming Algorithm to Solve the Poly Knapsack (Ubounded) Problem

Knapsack Problems

• Teaching Kids Programming - 0/1 Knapsack: Length of the Longest Subsequence That Sums to Target (Recursion+Memoization=Top Down Dynamic Programming)
• Teaching Kids Programming - 0/1 Knapsack Space Optimised Dynamic Programming Algorithm
• Teaching Kids Programming - Using Bottom Up Dynamic Programming Algorithm to Solve 0/1 Knapsack Problem
• Teaching Kids Programming - 0/1 Knapsack Problem via Top Down Dynamic Programming Algorithm
• Teaching Kids Programming - Multiple Strange Coin Flips/Toss Bottom Up Dynamic Programming Algorithm (Knapsack Variant)
• Teaching Kids Programming - Multiple Strange Coin Flips/Toss Top Down Dynamic Programming Algorithm (Knapsack Variant)
• Teaching Kids Programming - Max Profit of Rod Cutting (Unbounded Knapsack) via Bottom Up Dynamic Programming Algorithm
• Teaching Kids Programming - Max Profit of Rod Cutting (Unbounded Knapsack) via Top Down Dynamic Programming Algorithm
• Teaching Kids Programming - Brick Layout (Unlimited Knapsack) via Bottom Up Dynamic Programming Algorithm
• Teaching Kids Programming - Brick Layout (Unlimited Knapsack) via Top Down Dynamic Programming Algorithm
• Count Multiset Sum (Knapsacks) by Dynamic Programming Algorithm
• Count Multiset Sum (Knapsacks) by Recursive BackTracking Algorithm
• Dynamic Programming Algorithm to Solve the Poly Knapsack (Ubounded) Problem
• Dynamic Programming Algorithm to Solve 0-1 Knapsack Problem
• Classic Unlimited Knapsack Problem Variant: Coin Change via Dynamic Programming and Depth First Search Algorithm
• Classic Knapsack Problem Variant: Coin Change via Dynamic Programming and Breadth First Search Algorithm
• Complete Knapsack Problem
• 0/1 Knapsack Problem
• Teaching Kids Programming - Combination Sum Up to Target (Unique Numbers) by Dynamic Programming Algorithms
• Algorithms Series: 0/1 BackPack - Dynamic Programming and BackTracking
• Using BackTracking Algorithm to Find the Combination Integer Sum
• Facing Heads Probabilties of Tossing Strange Coins using Dynamic Programming Algorithm
• Partition Equal Subset Sum Algorithms using DFS, Top-Down and Bottom-up DP

–EOF (The Ultimate Computing & Technology Blog) —