Just Another Sudoku Solver in Depth First Search (and BackTracking) Algorithm

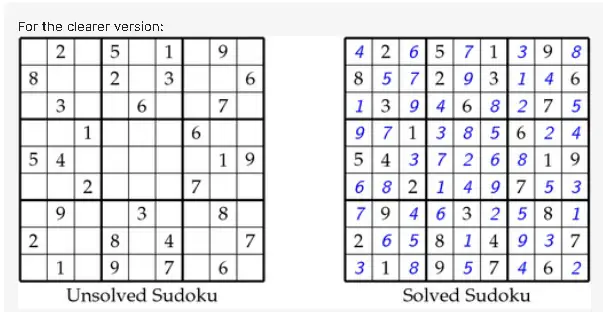
Sudoku is a puzzle where you’re given a partially-filled 9 by 9 grid with digits. The objective is to fill the grid with the constraint that every row, column, and box (3 by 3 subgrid) must contain all of the digits from 1 to 9. Implement an efficient sudoku solver that takes in an incomplete board and solves it. In the given board, the incomplete spaces will be 0.

Constraints
n = 9 where n is the number of rows and columns in matrix

Example 1
Input

matrix = [
    [0, 2, 0, 5, 0, 1, 0, 9, 0],
    [8, 0, 0, 2, 0, 3, 0, 0, 6],
    [0, 3, 0, 0, 6, 0, 0, 7, 0],
    [0, 0, 1, 0, 0, 0, 6, 0, 0],
    [5, 4, 0, 0, 0, 0, 0, 1, 9],
    [0, 0, 2, 0, 0, 0, 7, 0, 0],
    [0, 9, 0, 0, 3, 0, 0, 8, 0],
    [2, 0, 0, 8, 0, 4, 0, 0, 7],
    [0, 1, 0, 9, 0, 7, 0, 6, 0]
]

matrix = [
    [0, 2, 0, 5, 0, 1, 0, 9, 0],
    [8, 0, 0, 2, 0, 3, 0, 0, 6],
    [0, 3, 0, 0, 6, 0, 0, 7, 0],
    [0, 0, 1, 0, 0, 0, 6, 0, 0],
    [5, 4, 0, 0, 0, 0, 0, 1, 9],
    [0, 0, 2, 0, 0, 0, 7, 0, 0],
    [0, 9, 0, 0, 3, 0, 0, 8, 0],
    [2, 0, 0, 8, 0, 4, 0, 0, 7],
    [0, 1, 0, 9, 0, 7, 0, 6, 0]
]

Output

[
    [4, 2, 6, 5, 7, 1, 3, 9, 8],
    [8, 5, 7, 2, 9, 3, 1, 4, 6],
    [1, 3, 9, 4, 6, 8, 2, 7, 5],
    [9, 7, 1, 3, 8, 5, 6, 2, 4],
    [5, 4, 3, 7, 2, 6, 8, 1, 9],
    [6, 8, 2, 1, 4, 9, 7, 5, 3],
    [7, 9, 4, 6, 3, 2, 5, 8, 1],
    [2, 6, 5, 8, 1, 4, 9, 3, 7],
    [3, 1, 8, 9, 5, 7, 4, 6, 2]
]

[
    [4, 2, 6, 5, 7, 1, 3, 9, 8],
    [8, 5, 7, 2, 9, 3, 1, 4, 6],
    [1, 3, 9, 4, 6, 8, 2, 7, 5],
    [9, 7, 1, 3, 8, 5, 6, 2, 4],
    [5, 4, 3, 7, 2, 6, 8, 1, 9],
    [6, 8, 2, 1, 4, 9, 7, 5, 3],
    [7, 9, 4, 6, 3, 2, 5, 8, 1],
    [2, 6, 5, 8, 1, 4, 9, 3, 7],
    [3, 1, 8, 9, 5, 7, 4, 6, 2]
]

sudoku Just Another Sudoku Solver in Depth First Search (and BackTracking) Algorithm algorithms c / c++ games python

Unsolved and Solved Sudoku Game

Sudoku Solved using Depth First Search (BackTracking) Algorithm

We can use Depth First Search Algorithm to Solve Sudoku. The keys are to find violations and backtrack when needed. We can use the hash sets to store the numbers that have appeared in 9 rows, 9 columns, and 9 squares.

If we find a number that cannot be used, we simply skip it without continue placing. If we can place this number, we can Depth First Search into the next cell until we have completed the 81 numbers. If a current cell has been pre-filled with numbers, we would just go directly into next cell.

Remember we have to scan the board once to fill the hash sets (find out which digits are in which rows, cols, and each square).

Also restore the cell status (reset to zero), removing the digit from rows, cols and square hash sets when we backtrack.

Python Sudoku Solver

class Solution:
    def solve(self, matrix):
        def dfs(matrix, idx, rows, cols, boxes):
            if idx == 81:
                return True
            r = idx // 9
            c = idx % 9
            br = r // 3
            bc = c // 3
            if matrix[r][c] != 0:
                return dfs(matrix, idx + 1, rows, cols, boxes)
            for i in range(1, 10):
                if i in rows[r]:
                    continue
                if i in cols[c]:
                    continue
                if i in boxes[br][bc]:
                    continue
                rows[r].add(i)
                cols[c].add(i)
                boxes[br][bc].add(i)
                matrix[r][c] = i            
                if dfs(matrix, idx + 1, rows, cols, boxes):
                    return True                    
                matrix[r][c] = 0
                rows[r].remove(i)
                cols[c].remove(i)
                boxes[br][bc].remove(i)
            return False
        rows = [set() for _ in range(9)]
        cols = [set() for _ in range(9)]
        boxes = [[set() for _ in range(3)] for _ in range(3)]
        for r in range(9):
            for c in range(9):
                if matrix[r][c] != 0:
                    rows[r].add(matrix[r][c])
                    cols[c].add(matrix[r][c])
                    boxes[r//3][c//3].add(matrix[r][c])
        if dfs(matrix, 0, rows, cols, boxes):
            return matrix
        return None

class Solution:
    def solve(self, matrix):
        def dfs(matrix, idx, rows, cols, boxes):
            if idx == 81:
                return True
            r = idx // 9
            c = idx % 9
            br = r // 3
            bc = c // 3
            if matrix[r][c] != 0:
                return dfs(matrix, idx + 1, rows, cols, boxes)
            for i in range(1, 10):
                if i in rows[r]:
                    continue
                if i in cols[c]:
                    continue
                if i in boxes[br][bc]:
                    continue
                rows[r].add(i)
                cols[c].add(i)
                boxes[br][bc].add(i)
                matrix[r][c] = i            
                if dfs(matrix, idx + 1, rows, cols, boxes):
                    return True                    
                matrix[r][c] = 0
                rows[r].remove(i)
                cols[c].remove(i)
                boxes[br][bc].remove(i)
            return False
        rows = [set() for _ in range(9)]
        cols = [set() for _ in range(9)]
        boxes = [[set() for _ in range(3)] for _ in range(3)]
        for r in range(9):
            for c in range(9):
                if matrix[r][c] != 0:
                    rows[r].add(matrix[r][c])
                    cols[c].add(matrix[r][c])
                    boxes[r//3][c//3].add(matrix[r][c])
        if dfs(matrix, 0, rows, cols, boxes):
            return matrix
        return None

C++ Sudoku Solver

vector<vector<int>> solve(vector<vector<int>>& matrix) {
    function<bool(int, vector<unordered_set<int>>&, vector<unordered_set<int>>&, vector<vector<unordered_set<int>>>&)> dfs = 
    [&](int idx, vector<unordered_set<int>>& rows, vector<unordered_set<int>>& cols, vector<vector<unordered_set<int>>>& boxes) {
        if (idx == 81) {
            return true;
        }
        int row = idx / 9;
        int col = idx % 9;
        if (matrix[row][col] != 0) {
            return dfs(idx + 1, rows, cols, boxes);
        }
        int boxR = row / 3;
        int boxC = col / 3;
        for (int i = 1; i <= 9; ++ i) {
            if (rows[row].count(i)) continue;
            if (cols[col].count(i)) continue;
            if (boxes[boxR][boxC].count(i)) continue;
            rows[row].insert(i);
            cols[col].insert(i);
            boxes[boxR][boxC].insert(i);
            matrix[row][col] = i;
            if (dfs(idx + 1, rows, cols, boxes)) {
                return true;
            }
            matrix[row][col] = 0;
            rows[row].erase(i);
            cols[col].erase(i);
            boxes[boxR][boxC].erase(i);
        }
        return false;
    };
    vector<unordered_set<int>> rows(9);
    vector<unordered_set<int>> cols(9);
    vector<vector<unordered_set<int>>> boxes(3, vector<unordered_set<int>>(3));
    for (int r = 0; r < 9; ++ r) {
        for (int c = 0; c < 9; ++ c) {
            if (matrix[r][c] == 0) continue;
            rows[r].insert(matrix[r][c]);
            cols[c].insert(matrix[r][c]);
            boxes[r/3][c/3].insert(matrix[r][c]);
        }
    }
    if (dfs(0, rows, cols, boxes)) {
        return matrix;
    }
    return {{}};
}

vector<vector<int>> solve(vector<vector<int>>& matrix) {
    function<bool(int, vector<unordered_set<int>>&, vector<unordered_set<int>>&, vector<vector<unordered_set<int>>>&)> dfs = 
    [&](int idx, vector<unordered_set<int>>& rows, vector<unordered_set<int>>& cols, vector<vector<unordered_set<int>>>& boxes) {
        if (idx == 81) {
            return true;
        }
        int row = idx / 9;
        int col = idx % 9;
        if (matrix[row][col] != 0) {
            return dfs(idx + 1, rows, cols, boxes);
        }
        int boxR = row / 3;
        int boxC = col / 3;
        for (int i = 1; i <= 9; ++ i) {
            if (rows[row].count(i)) continue;
            if (cols[col].count(i)) continue;
            if (boxes[boxR][boxC].count(i)) continue;
            rows[row].insert(i);
            cols[col].insert(i);
            boxes[boxR][boxC].insert(i);
            matrix[row][col] = i;
            if (dfs(idx + 1, rows, cols, boxes)) {
                return true;
            }
            matrix[row][col] = 0;
            rows[row].erase(i);
            cols[col].erase(i);
            boxes[boxR][boxC].erase(i);
        }
        return false;
    };
    vector<unordered_set<int>> rows(9);
    vector<unordered_set<int>> cols(9);
    vector<vector<unordered_set<int>>> boxes(3, vector<unordered_set<int>>(3));
    for (int r = 0; r < 9; ++ r) {
        for (int c = 0; c < 9; ++ c) {
            if (matrix[r][c] == 0) continue;
            rows[r].insert(matrix[r][c]);
            cols[c].insert(matrix[r][c]);
            boxes[r/3][c/3].insert(matrix[r][c]);
        }
    }
    if (dfs(0, rows, cols, boxes)) {
        return matrix;
    }
    return {{}};
}

–EOF (The Ultimate Computing & Technology Blog) —

GD Star Rating
loading...

820 words
Last Post: Teaching Kids Programming - Dynamic Programming Algorithms to Compute the Least Number of Perfect Squares
Next Post: Teaching Kids Programming - Longest Increasing Subsequence via Dynamic Programming Algorithm

The Permanent URL is: Just Another Sudoku Solver in Depth First Search (and BackTracking) Algorithm

Algorithms, Blockchain and Cloud

Just Another Sudoku Solver in Depth First Search (and BackTracking) Algorithm

Sudoku Solved using Depth First Search (BackTracking) Algorithm

Python Sudoku Solver

C++ Sudoku Solver

Leave a Reply

Sudoku Solved using Depth First Search (BackTracking) Algorithm

Python Sudoku Solver

C++ Sudoku Solver

Related posts:

Leave a Reply