Home
Partition Equal Subset Sum Algorithms using DFS, Top-Down and Bottom-up DP
Tags:, , , , ,

Partition Equal Subset Sum Algorithms using DFS, Top-Down and Bottom-up DP

October 10, 2020 No Comments algorithms, c / c++, DFS, dynamic programming, Dynamic Programming, Knapsack Problems, math, recursive

Given a non-empty array nums containing only positive integers, find if the array can be partitioned into two subsets such that the sum of elements in both subsets is equal.

Example 1:
Input: nums = [1,5,11,5]
Output: true
Explanation: The array can be partitioned as [1, 5, 5] and [11].

Example 2:
Input: nums = [1,2,3,5]

Output: false
Explanation: The array cannot be partitioned into equal sum subsets.

Constraints:
1 <= nums.length <= 200
1 <= nums[i] <= 100

We know that if the total sum of all numbers in the array is odd, we can’t parition such array into two equal subset. We can just using Depth First Search (Bruteforce without optimisation), Top-down Dynamic Programming (sometimes aka Top-Down DFS with Memoization), and Bottom Up Dynamic Programming Algorithm.

Bruteforce with Depth First Search Algorithm

First, we compute the sum, then we can perform a bruteforce search with the DFS recursively. The sum is passed on to next recursion until we either exhaust the options or we have partial sum that is more than half of the total sum.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        sum = std::accumulate(begin(nums), end(nums), 0, [](auto &a, auto &b) {
            return a + b;
        });
        if (sum & 1) return false;
        return dfs(nums, 0, 0);
    }
 
private:
    int sum;
    bool dfs(vector<int> &nums, int curSum, int left) {
        if (curSum + curSum == sum) {
            return true;
        }
        if (curSum + curSum > sum) {
            return false;
        }
        for (int i = left; i < nums.size(); ++ i) {
            if (dfs(nums, curSum + nums[i], i + 1)) {
                return true;
            }
        }
        return false;
    }
};
class Solution {
public:
    bool canPartition(vector<int>& nums) {
        sum = std::accumulate(begin(nums), end(nums), 0, [](auto &a, auto &b) {
            return a + b;
        });
        if (sum & 1) return false;
        return dfs(nums, 0, 0);
    }

private:
    int sum;
    bool dfs(vector<int> &nums, int curSum, int left) {
        if (curSum + curSum == sum) {
            return true;
        }
        if (curSum + curSum > sum) {
            return false;
        }
        for (int i = left; i < nums.size(); ++ i) {
            if (dfs(nums, curSum + nums[i], i + 1)) {
                return true;
            }
        }
        return false;
    }
};

We use the std::accumulate to calculate the total sum without using a for/while loop. The Depth First Search exhausts all possible combination which times up to O(2^n) where N is the number of elements in the array. For each number, we can either pick it or skip it.

Top-Down Dynamic Programming Algorithm via DFS + Memoization

We can improve the above Depth First Search Algorithm by using the Memoization technique (storing the intermediate answers in hash table). This is sometimes known as the Top-Down Dynamic Programming Algorithm where we store the answers and re-use them later.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        sum = std::accumulate(begin(nums), end(nums), 0, [](auto &a, auto &b) {
            return a + b;
        });
        if (sum & 1) return false;
        return dfs(nums, 0, 0);
    }
 
private:
    int sum;
    unordered_map<int, bool> memo;
    
    bool dfs(vector<int> &nums, int curSum, int left) {
        if (curSum + curSum == sum) {
            return true;
        }
        if (curSum + curSum > sum) {
            return false;
        }
        if (memo.find(curSum) != memo.end()) {
            return memo[curSum]; // re-use the answer if it is calculated before
        }
        for (int i = left; i < nums.size(); ++ i) {
            if (dfs(nums, curSum + nums[i], i + 1)) {
                memo[curSum] = true; // storing in hash table
                return true;
            }
        }
        memo[curSum] = false; // storing in hash table
        return false;
    }
};
class Solution {
public:
    bool canPartition(vector<int>& nums) {
        sum = std::accumulate(begin(nums), end(nums), 0, [](auto &a, auto &b) {
            return a + b;
        });
        if (sum & 1) return false;
        return dfs(nums, 0, 0);
    }

private:
    int sum;
    unordered_map<int, bool> memo;
    
    bool dfs(vector<int> &nums, int curSum, int left) {
        if (curSum + curSum == sum) {
            return true;
        }
        if (curSum + curSum > sum) {
            return false;
        }
        if (memo.find(curSum) != memo.end()) {
            return memo[curSum]; // re-use the answer if it is calculated before
        }
        for (int i = left; i < nums.size(); ++ i) {
            if (dfs(nums, curSum + nums[i], i + 1)) {
                memo[curSum] = true; // storing in hash table
                return true;
            }
        }
        memo[curSum] = false; // storing in hash table
        return false;
    }
};

The time complexity is still O(2^n) in the worst case as we might calculate the unique sub-sum everytime. However, in practice, this approach is generally acceptable.

The space requirement is O(N) where N is the number of the subsum.

Bottom-up Dynamic Programming Algorithm to Partition Equal Subset Sum

Let’s consider the Dynamic Programming formula: dp[i] stores if subsum can be formed using the numbers in the array. The inital dp[0] = true and we could iterate all the numbers and then check for subsum up to half:

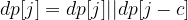tex_8b498fe20f8ccf62affbbd2752a2655b Partition Equal Subset Sum Algorithms using DFS, Top-Down and Bottom-up DP algorithms c / c++ DFS dynamic programming Dynamic Programming Knapsack Problems math recursive for j between [c..half] and [c in nums].

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int totalSum = std::accumulate(begin(nums), end(nums), 0, [](auto &a, auto &b) {
            return a + b;
        });
        if (totalSum & 1) return false;
        int half = totalSum >> 1;
        int n = nums.size();
        vector<bool> dp(half + 1, false);
        dp[0] = true;
        for (auto curr : nums) {
            for (int j = half; j >= curr; j--) {
                dp[j] = dp[j] || dp[j - curr];
            }
        }
        return dp[half];
    }
};
class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int totalSum = std::accumulate(begin(nums), end(nums), 0, [](auto &a, auto &b) {
            return a + b;
        });
        if (totalSum & 1) return false;
        int half = totalSum >> 1;
        int n = nums.size();
        vector<bool> dp(half + 1, false);
        dp[0] = true;
        for (auto curr : nums) {
            for (int j = half; j >= curr; j--) {
                dp[j] = dp[j] || dp[j - curr];
            }
        }
        return dp[half];
    }
};

The time complexity is O(M.N) and the space rquirement is O(N) where N is the sum of all numbers divided by two.

Knapsack Problems

–EOF (The Ultimate Computing & Technology Blog) —

GD Star Rating
loading...
881 words
Last Post: Depth First Search Algorithm to Check If Two Expression Trees are Equivalent
Next Post: Algorithm to Compute the Maximum Nesting Depth of the Parentheses

The Permanent URL is: Partition Equal Subset Sum Algorithms using DFS, Top-Down and Bottom-up DP

Related posts:

  1. SQL Coding Exercise – Delete Duplicate Emails Write a SQL query to delete all duplicate email entries in a table named Person,...
  2. Teaching Kids Programming – Find Partition Equal Subset Sum (Top Down Dynamic Programming Algorithm) Teaching Kids Programming: Videos on Data Structures and Algorithms Given a non-empty array nums containing...
  3. Teaching Kids Programming – Longest Strictly Increasing Then Decreasing Sublist Teaching Kids Programming: Videos on Data Structures and Algorithms You are given a list of...
  4. Teaching Kids Programming – Max Profit of Rod Cutting (Unbounded Knapsack) via Bottom Up Dynamic Programming Algorithm Teaching Kids Programming: Videos on Data Structures and Algorithms You are given a list of...
  5. Teaching Kids Programming – Form Smallest Number From Two Digit Arrays (Set Intersection) Teaching Kids Programming: Videos on Data Structures and Algorithms Given two arrays of unique digits...
  6. Teaching Kids Programming – Probability Matrix of Walking in a Grid (Unique Paths) Teaching Kids Programming: Videos on Data Structures and Algorithms On a grid that each step,...
  7. Teaching Kids Programming – Back Tracking Algorithm to Find the The Knight’s Tour Path (Recursive Depth First Search) Teaching Kids Programming: Videos on Data Structures and Algorithms Given two positive integers m and...
  8. Azure Subscription Cost Vary Due to “Standard SSD Managed – Disk Operations” Difference I have noticed in the last two months, the cost of my Azure Subscription is...

Leave a Reply