Teaching Kids Programming – Using Bottom Up Dynamic Programming Algorithm to Solve 0/1 Knapsack Problem

Teaching Kids Programming: Videos on Data Structures and Algorithms

You are given two lists of integers weights and values which have the same length and an integer capacity. weights[i] and values[i] represent the weight and value of the ith item. Given that you can take at most capacity weights, and that you can only take at most one copy of each item, return the maximum amount of value you can get.

Constraints
n ≤ 250 where n is the length of weights and values
capacity ≤ 250

Example 1
Input
weights = [1, 2, 3]
values = [1, 5, 3]
capacity = 5
Output
8
Similar to original knapsack, but how do you ensure the specific element is only included once?

0/1 Knapsack Problem via Bottom Up Dynamic Programming Algorithm

We can describe the 0/1 Knapsack problem via the following Math terms:

Given a knapsack with capacity 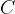and 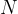items to pack with weights 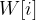and values .
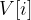We want to pack items into the knapsack subject to total weights not exceeding the capacity.

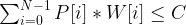
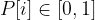meaning the quantity of each item we are to pick.
We want to meantime maximize the values .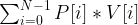

The Dynamic Programming Equation is:

If 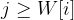the capacity j is enough to pick item i.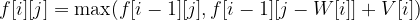
Otherwise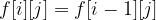

We can solve this DP using Top Down Dynamic Programming aka Recursion with Memoization: Teaching Kids Programming – 0/1 Knapsack Problem via Top Down Dynamic Programming Algorithm

Alternatively, we can proactively store the values in a two dimensional array. We need to compute the values of the first row e.g. dp[0][i] for i in range(c). If i (capacity) is larger or equal than the first item’s weight, we can set the value to v[0]. Otherwise, the value gain would be zero.

Then, we start filling the values from the second row up to the last row e.g. dp[n-1].

1
2
3
4
5
6
7
8
9
10
11
12
13

class Solution:
    def knapsack01(self, weights, values, capacity):
        n = len(weights)
 
        dp = [[0 for _ in range(capacity + 1)] for _ in range(n)]
        for i in range(capacity + 1):
            dp[0][i] = 0 if weights[0] > i else values[0]
 
        for i in range(1, n):
            for j in range(1, capacity + 1):
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weights[i]] + values[i] if j >= weights[i] else 0)
 
        return dp[n - 1][capacity]

class Solution:
    def knapsack01(self, weights, values, capacity):
        n = len(weights)

        dp = [[0 for _ in range(capacity + 1)] for _ in range(n)]
        for i in range(capacity + 1):
            dp[0][i] = 0 if weights[0] > i else values[0]

        for i in range(1, n):
            for j in range(1, capacity + 1):
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weights[i]] + values[i] if j >= weights[i] else 0)

        return dp[n - 1][capacity]

The time and space complexity is O(NC) – same as Top Down Dynamic Programming Implementation. However, practically speaking, the Bottom Up Dynamic Programming is faster.

Knapsack Problems

• Teaching Kids Programming - 0/1 Knapsack: Length of the Longest Subsequence That Sums to Target (Recursion+Memoization=Top Down Dynamic Programming)
• Teaching Kids Programming - 0/1 Knapsack Space Optimised Dynamic Programming Algorithm
• Teaching Kids Programming - Using Bottom Up Dynamic Programming Algorithm to Solve 0/1 Knapsack Problem
• Teaching Kids Programming - 0/1 Knapsack Problem via Top Down Dynamic Programming Algorithm
• Teaching Kids Programming - Multiple Strange Coin Flips/Toss Bottom Up Dynamic Programming Algorithm (Knapsack Variant)
• Teaching Kids Programming - Multiple Strange Coin Flips/Toss Top Down Dynamic Programming Algorithm (Knapsack Variant)
• Teaching Kids Programming - Max Profit of Rod Cutting (Unbounded Knapsack) via Bottom Up Dynamic Programming Algorithm
• Teaching Kids Programming - Max Profit of Rod Cutting (Unbounded Knapsack) via Top Down Dynamic Programming Algorithm
• Teaching Kids Programming - Brick Layout (Unlimited Knapsack) via Bottom Up Dynamic Programming Algorithm
• Teaching Kids Programming - Brick Layout (Unlimited Knapsack) via Top Down Dynamic Programming Algorithm
• Count Multiset Sum (Knapsacks) by Dynamic Programming Algorithm
• Count Multiset Sum (Knapsacks) by Recursive BackTracking Algorithm
• Dynamic Programming Algorithm to Solve the Poly Knapsack (Ubounded) Problem
• Dynamic Programming Algorithm to Solve 0-1 Knapsack Problem
• Classic Unlimited Knapsack Problem Variant: Coin Change via Dynamic Programming and Depth First Search Algorithm
• Classic Knapsack Problem Variant: Coin Change via Dynamic Programming and Breadth First Search Algorithm
• Complete Knapsack Problem
• 0/1 Knapsack Problem
• Teaching Kids Programming - Combination Sum Up to Target (Unique Numbers) by Dynamic Programming Algorithms
• Algorithms Series: 0/1 BackPack - Dynamic Programming and BackTracking
• Using BackTracking Algorithm to Find the Combination Integer Sum
• Facing Heads Probabilties of Tossing Strange Coins using Dynamic Programming Algorithm
• Partition Equal Subset Sum Algorithms using DFS, Top-Down and Bottom-up DP

–EOF (The Ultimate Computing & Technology Blog) —