Teaching Kids Programming – 0/1 Knapsack Problem via Top Down Dynamic Programming Algorithm

Teaching Kids Programming: Videos on Data Structures and Algorithms

You are given two lists of integers weights and values which have the same length and an integer capacity. weights[i] and values[i] represent the weight and value of the ith item. Given that you can take at most capacity weights, and that you can only take at most one copy of each item, return the maximum amount of value you can get.

Constraints
n ≤ 250 where n is the length of weights and values
capacity ≤ 250

Example 1
Input
weights = [1, 2, 3]
values = [1, 5, 3]
capacity = 5
Output
8
Similar to original knapsack, but how do you ensure the specific element is only included once?

0/1 Knapsack Problem via Top Down Dynamic Programming Algorithm

This problem can be expressed in the following math terms:

Given N items: 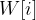(i from 0 to N-1 inclusive) represents the weight for each item.
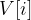(i from 0 to N-1 inclusive) is the value for each item.
And 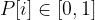where 0 means we do not pick i-th item and 1 means we pick it.

We want to maximize the profit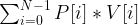
subject to 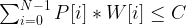where C is the maximum capacity of the knapsack

The greedy approach (Picking the most valuable items) does not work: for example we could have a item which exceeds the capacity but very valuable. Another greedy approach would be to pick the items with the most value/weight ratio but this doesn’t work either considering the following:

weights = [1, 2, 3] and values = [2, 5, 3], capacity = 5
so the v2w wouild be [2, 2.5, 1] and we need to pick the first two items according to the strategy which will give us total value = 7 and remaining capacity is 5-(1+2)=2
The optimal would be to pick last two items total weight = 2+3=5 (less or equal to total capacity 5) and total value is 5+3=8

We can bruteforce – there are subsequences with each item we can pick or not pick. And it takes O(N) time to compute the total weight thus total time complexity is which is exponential.

We can use the Top Down Dynamic Programming Algorithm to compute the maximal value we can get – each item we have two choices pick or not pick, and we can remember the max values at that point – via the Recursion + Memoization aka @cache.

If the remaining capacity is larger than the current items’ weight – we can try to pick this item. dfs(i, c) means we are making a decision to pick i-th item when the knapsack has c remaining capacity.

1
2
3
4
5
6
7
8
9
10
11
12
13
14

class Solution:
    def knapsack01(self, weights, values, capacity):
        
        @cache
        def dfs(i, c):
            if i < 0:
                return 0
            ans = 0
            if c >= weights[i]:
                ans = max(ans, dfs(i - 1, c - weights[i]) + values[i])
            ans = max(ans, dfs(i - 1, c))
            return ans
 
        return dfs(len(values) - 1, capacity)

class Solution:
    def knapsack01(self, weights, values, capacity):
        
        @cache
        def dfs(i, c):
            if i < 0:
                return 0
            ans = 0
            if c >= weights[i]:
                ans = max(ans, dfs(i - 1, c - weights[i]) + values[i])
            ans = max(ans, dfs(i - 1, c))
            return ans

        return dfs(len(values) - 1, capacity)

We can start from the index 0 – first item, and it would work too.

1
2
3
4
5
6
7
8
9
10
11
12
13
14

class Solution:
    def knapsack01(self, weights, values, capacity):
        
        @cache
        def dfs(i, c):
            if i == len(values):
                return 0
            ans = 0
            if c >= weights[i]:
                ans = max(ans, dfs(i + 1, c - weights[i]) + values[i])
            ans = max(ans, dfs(i + 1, c))
            return ans
 
        return dfs(0, capacity)

class Solution:
    def knapsack01(self, weights, values, capacity):
        
        @cache
        def dfs(i, c):
            if i == len(values):
                return 0
            ans = 0
            if c >= weights[i]:
                ans = max(ans, dfs(i + 1, c - weights[i]) + values[i])
            ans = max(ans, dfs(i + 1, c))
            return ans

        return dfs(0, capacity)

The time complexity and space complexity is O(CN) as we are using @cache and each state is calculated only once.

Knapsack Problems

• Teaching Kids Programming - 0/1 Knapsack: Length of the Longest Subsequence That Sums to Target (Recursion+Memoization=Top Down Dynamic Programming)
• Teaching Kids Programming - 0/1 Knapsack Space Optimised Dynamic Programming Algorithm
• Teaching Kids Programming - Using Bottom Up Dynamic Programming Algorithm to Solve 0/1 Knapsack Problem
• Teaching Kids Programming - 0/1 Knapsack Problem via Top Down Dynamic Programming Algorithm
• Teaching Kids Programming - Multiple Strange Coin Flips/Toss Bottom Up Dynamic Programming Algorithm (Knapsack Variant)
• Teaching Kids Programming - Multiple Strange Coin Flips/Toss Top Down Dynamic Programming Algorithm (Knapsack Variant)
• Teaching Kids Programming - Max Profit of Rod Cutting (Unbounded Knapsack) via Bottom Up Dynamic Programming Algorithm
• Teaching Kids Programming - Max Profit of Rod Cutting (Unbounded Knapsack) via Top Down Dynamic Programming Algorithm
• Teaching Kids Programming - Brick Layout (Unlimited Knapsack) via Bottom Up Dynamic Programming Algorithm
• Teaching Kids Programming - Brick Layout (Unlimited Knapsack) via Top Down Dynamic Programming Algorithm
• Count Multiset Sum (Knapsacks) by Dynamic Programming Algorithm
• Count Multiset Sum (Knapsacks) by Recursive BackTracking Algorithm
• Dynamic Programming Algorithm to Solve the Poly Knapsack (Ubounded) Problem
• Dynamic Programming Algorithm to Solve 0-1 Knapsack Problem
• Classic Unlimited Knapsack Problem Variant: Coin Change via Dynamic Programming and Depth First Search Algorithm
• Classic Knapsack Problem Variant: Coin Change via Dynamic Programming and Breadth First Search Algorithm
• Complete Knapsack Problem
• 0/1 Knapsack Problem
• Teaching Kids Programming - Combination Sum Up to Target (Unique Numbers) by Dynamic Programming Algorithms
• Algorithms Series: 0/1 BackPack - Dynamic Programming and BackTracking
• Using BackTracking Algorithm to Find the Combination Integer Sum
• Facing Heads Probabilties of Tossing Strange Coins using Dynamic Programming Algorithm
• Partition Equal Subset Sum Algorithms using DFS, Top-Down and Bottom-up DP

We can also solve this 0/1 Knapsack problem via Bottom Up Dynamic Programming Algorithm where we proactively compute the values and store in a two dimensional array in the bottom up manner e.g. i=0,j=0 dp[i][j]: Teaching Kids Programming – 0/1 Knapsack Problem via Bottom Up Dynamic Programming Algorithm

–EOF (The Ultimate Computing & Technology Blog) —