Teaching Kids Programming – Algorithms to Count Total Number of Colored Cells (Math/Recursion/Dynamic Programming)

Teaching Kids Programming: Videos on Data Structures and Algorithms

There exists an infinitely large two-dimensional grid of uncolored unit cells. You are given a positive integer n, indicating that you must do the following routine for n minutes:

At the first minute, color any arbitrary unit cell blue.
Every minute thereafter, color blue every uncolored cell that touches a blue cell.
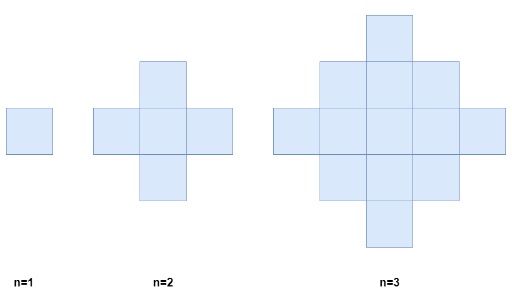
Below is a pictorial representation of the state of the grid after minutes 1, 2, and 3.

Count Total Number of Colored Cells

Return the number of colored cells at the end of n minutes.

Example 1:
Input: n = 1
Output: 1
Explanation: After 1 minute, there is only 1 blue cell, so we return 1.

Example 2:
Input: n = 2
Output: 5
Explanation: After 2 minutes, there are 4 colored cells on the boundary and 1 in the center, so we return 5.

Constraints:
1 <= n <= 10^5

Algorithms to Count Total Number of Colored Cells

We can solve this problem by using recursion and math. By observing the pattern for the first few numbers, we see these (assume f(n) is the answer i.e. the total number of cells after n minutes)

F(1) = 1
F(2) = 5
F(3) = 13
F(4) = 25
F(5) = 41
…

Recursion Formula

We have the following Recursive Formula:

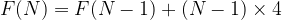
We interpret this:

The N-th minute equals the number of the cells at N-1 minute which is F(N-1) plus the (N-2)*4 cells on the shoulder, and plus 4 cells (top, bottom, left and right).

So: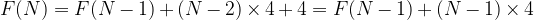

See below: the “0” is F(1) – and F(2) equals F(1) plus the (2-1)*4 X’s, and plus 4 Y’s.

    Y
  X 0 X
Y 0 0 0 Y
  X 0 X
    Y

With this Recursive equation, we can implement using Recursion, Bottom Up or Top Down Dynamic Programming methods:

The Recursion with Memoization:

1
2
3
4
5
6

@cache
def f(n):
    if n == 1:
       return 1
    assert n > 1
    return f(n-1) * (n-1) * 4

@cache
def f(n):
    if n == 1:
       return 1
    assert n > 1
    return f(n-1) * (n-1) * 4

The bottom up Dynamic Programming solution:

1
2
3
4
5
6

def f(n):
    ans = 1
    for i in range(n):
        ans += i * 4
        ans += 4
    return ans

def f(n):
    ans = 1
    for i in range(n):
        ans += i * 4
        ans += 4
    return ans

Math

We see that the total number of cells can be computed as two arithmetic sequences: 1, 3, 5, 7, … 2N-1 and 1, 3, 5, 7, 2N-3.

We can then sum the arithmetic sequence (1, 3, 5, 7, … 2N-1) multiplied by two and subtract the middle one which is 2N-1.

The equation is: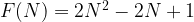

Then, we can implement the math solution using O(1) time and space – which is the optimal:

1
2

def f(n):
    return 2*n*n - 2*n + 1

def f(n):
    return 2*n*n - 2*n + 1

–EOF (The Ultimate Computing & Technology Blog) —