Teaching Kids Programming – Cascading Algorithm to Find All Subsets

Teaching Kids Programming: Videos on Data Structures and Algorithms

Given an integer array nums of unique elements, return all possible subsets (the power set). The solution set must not contain duplicate subsets. Return the solution in any order.

Example 1:
Input: nums = [1,2,3]
Output: [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

Example 2:
Input: nums = [0]
Output: [[],[0]]

Constraints:
1 <= nums.length <= 10
-10 <= nums[i] <= 10
All the numbers of nums are unique.

Cascading Algorithm to Find All Subsets

The idea of cascading is to iterate over the numbers and append each to the existing subsets as the new subsets. Therefore at each iteration, the size of subsets doubles. For example: consider [1,2,3].

ans = [[]]
take number 1: make a copy of all subsets [[]], and append 1 to them to make new subsets e.g. [1].
take number 2: make a copy of all subsets [[],[1]] and append 2 to them to make new subsets e.g. [2],[1,2]
take number 3: make a copy of all subsets [[],[1],[2],[1,2]] and append 3 to them which makes: [3],[1,3],[2,3],[1,2,3]

The following Python code implements the cascading algorithm to find all subsets given a list that consists of unique numbers. Both time and space complexity is .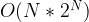

1
2
3
4
5
6
7

class Solution:
    def subsets(self, nums: list[int]) -> list[int]:        
        n = len(nums)
        ans = [[]]        
        for n in nums:
            ans += [c + [n] for c in ans]            
        return ans

class Solution:
    def subsets(self, nums: list[int]) -> list[int]:        
        n = len(nums)
        ans = [[]]        
        for n in nums:
            ans += [c + [n] for c in ans]            
        return ans

Subsets Algorithms

• Teaching Kids Programming – Finding All Subsets by Bitmasking Algorithm
• Teaching Kids Programming – Finding All Subsets via Backtracking Algorithm (Recursion / Depth First Search)
• Generate the Power SubSet using Depth First Search Algorithm
• Teaching Kids Programming – Cascading Algorithm to Find All Subsets

–EOF (The Ultimate Computing & Technology Blog) —