Teaching Kids Programming – Closest Leaf in a Binary Tree (Breadth/Depth First Search Algorithm in Graph)

Teaching Kids Programming: Videos on Data Structures and Algorithms

Given the root of a binary tree where every node has a unique value and a target integer k, return the value of the nearest leaf node to the target k in the tree.

Nearest to a leaf means the least number of edges traveled on the binary tree to reach any leaf of the tree. Also, a node is called a leaf if it has no children.

closest-leaf-to-node

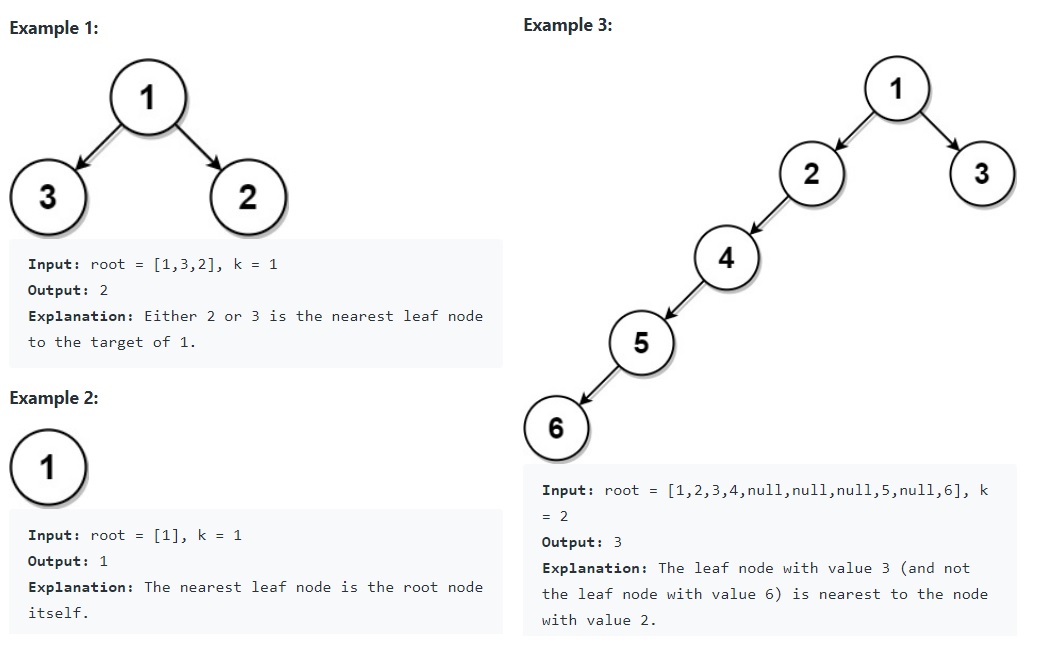
Example 1:
Input: root = [1,3,2], k = 1
Output: 2
Explanation: Either 2 or 3 is the nearest leaf node to the target of 1.

Example 2:
Input: root = [1], k = 1
Output: 1
Explanation: The nearest leaf node is the root node itself.

Example 3:
Input: root = [1,2,3,4,null,null,null,5,null,6], k = 2
Output: 3
Explanation: The leaf node with value 3 (and not the leaf node with value 6) is nearest to the node with value 2.

Constraints:
The number of nodes in the tree is in the range [1, 1000].
1 <= Node.val <= 1000
All the values of the tree are unique.
There exist some node in the tree where Node.val == k.

Hints:
Convert the tree to a general graph, and do a breadth-first search. Alternatively, find the closest leaf for every node on the path from root to target.

Closest Leaf in a Binary Tree (Breadth/Depth First Search in Graph)

First, we can convert the binary tree to a graph using the Adjacent List and the Recursive Depth First Search Algorithm (DFS) – which allows us to traverse between any two nodes in the tree. Then, we do a Breadth First Search Algorithm (BFS) on the Node K and stop when it hits a leaf. BFS or DFS on a tree does not require using a hash set to store the visited nodes because we can only traverse from parents to the children nodes. However, when BFS or DFS is applied in a Graph Data Structure, we need to avoid visiting same nodes multiple times, and a hash set is usually helpful.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def findClosestLeaf(self, root: Optional[TreeNode], k: int) -> int:
        
        G = defaultdict(list)
        leafs = set()
        
        def dfs(root, par):
            if not root:
                return
            dfs(root.left, root)
            dfs(root.right, root)
            if par:
                G[root.val].append(par.val)                
                G[par.val].append(root.val)
            if not root.left and not root.right:
                leafs.add(root.val)
            
        dfs(root, None)
        
        seen = set()
        q = deque([k])
        while q:
            cur = q.popleft()
            if cur in leafs:
                return cur
            for n in G[cur]:
                if n not in seen:
                    q.append(n)
                    seen.add(n)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def findClosestLeaf(self, root: Optional[TreeNode], k: int) -> int:
        
        G = defaultdict(list)
        leafs = set()
        
        def dfs(root, par):
            if not root:
                return
            dfs(root.left, root)
            dfs(root.right, root)
            if par:
                G[root.val].append(par.val)                
                G[par.val].append(root.val)
            if not root.left and not root.right:
                leafs.add(root.val)
            
        dfs(root, None)
        
        seen = set()
        q = deque([k])
        while q:
            cur = q.popleft()
            if cur in leafs:
                return cur
            for n in G[cur]:
                if n not in seen:
                    q.append(n)
                    seen.add(n)

The time/space complexity of above Algorithms is O(N) where N is the number of the nodes in the given binary tree. A tree with N nodes has N-1 edges.

–EOF (The Ultimate Computing & Technology Blog) —