Teaching Kids Programming – Dynamic Programming Algorithms to Count the Number of Unique Binary Search Trees (Catalan Numbers)

Teaching Kids Programming: Videos on Data Structures and Algorithms

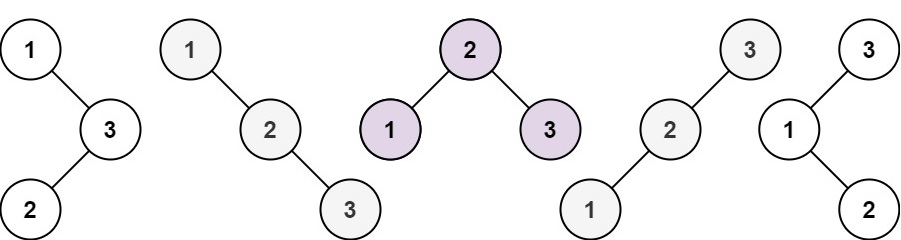
Given an integer n, return the number of structurally unique BST’s (binary search trees) which has exactly n nodes of unique values from 1 to n.

Unique Binary Search Trees

Example 1:
Input: n = 3
Output: 5

Example 2:
Input: n = 1
Output: 1

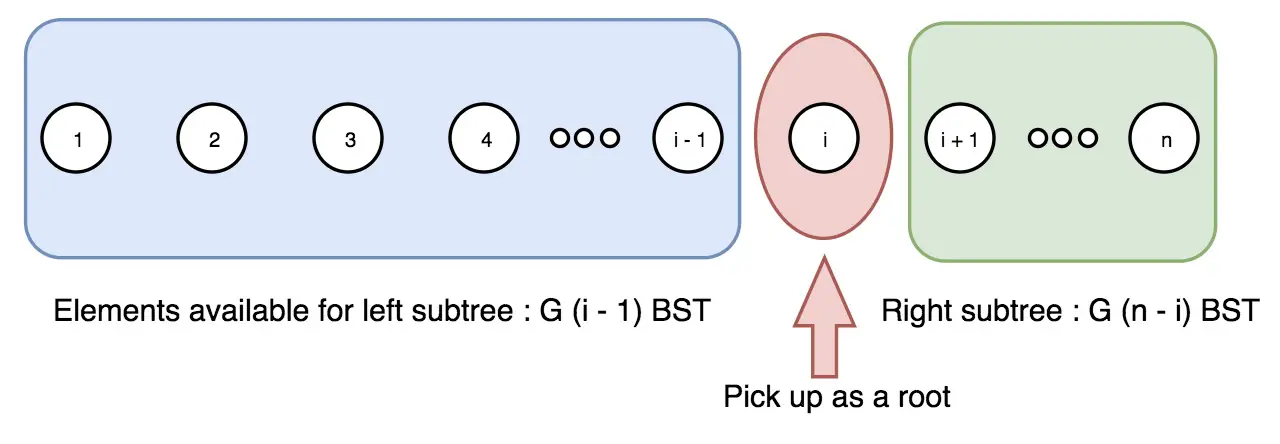
Given N nodes, let’s say, the number of unique Binary Search Trees (BSTs) is G(N). Also, let’s use F(i, N) to represent the number of BSTs with N nodes but also use i as the root.

cartesian product of the number of BST for its left and right subtrees, as illustrated below

Give i as the root, there is i-1 nodes on the left and n-i nodes on the right, which corresponds to G(i-1) and G(n-i)

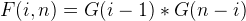
And, 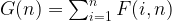, thus:

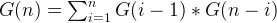
And we know G[0] = G[1] = 1.

Also, if the nodes are label from 0 to n-1 instead. We can shift the value a bit:

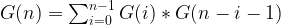
Top Down Dynamic Programming Algorithm to Compute the Catalan Number

We can implement the above DP equation using Top Down, with the help of Recursion and Memoziation via @cache.

1
2
3
4
5
6
7
8

class Solution:
    def numTrees(self, n):
        @cache
        def G(n):
            if n == 0:
                return 1
            return sum(G(i)*G(n-i-1) for i in range(n))
        return G(n)

class Solution:
    def numTrees(self, n):
        @cache
        def G(n):
            if n == 0:
                return 1
            return sum(G(i)*G(n-i-1) for i in range(n))
        return G(n)

The time complexity is O(N^2) as for each G value we have to compute a loop. And the space complexity is O(N) as we are caching G(0), G(1) to G(N-1) i.e. N values.

Bottom Up Dynamic Programming Algorithm to Compute the Catalan Number

We can compute the G values from G[0], G[1] bottom up to G[n]. The values will be stored using a list/array.

1
2
3
4
5
6
7
8

class Solution:
    def numTrees(self, n):
        G = [0]*(n+1)
        G[0] = 1
        for i in range(1, n+1):
            for j in range(i):
                G[i] += G[j] * G[i-j-1]
        return G[n]

class Solution:
    def numTrees(self, n):
        G = [0]*(n+1)
        G[0] = 1
        for i in range(1, n+1):
            for j in range(i):
                G[i] += G[j] * G[i-j-1]
        return G[n]

The time complexity is O(N^2) and the space complexity is O(N).

Catalan Numbers

It turns out the answer is the N-th Catalan numbers.

See also: How to Compute the Catalan Number?

–EOF (The Ultimate Computing & Technology Blog) —