Teaching Kids Programming – Gray Code by Recursive Mirror Algorithm

Teaching Kids Programming: Videos on Data Structures and Algorithms

An n-bit gray code sequence is a sequence of 2n integers where:

Every integer is in the inclusive range [0, 2n – 1],
The first integer is 0,
An integer appears no more than once in the sequence,
The binary representation of every pair of adjacent integers differs by exactly one bit, and
The binary representation of the first and last integers differs by exactly one bit.
Given an integer n, return any valid n-bit gray code sequence.

Example 1:
Input: n = 2
Output: [0,1,3,2]
Explanation:
The binary representation of [0,1,3,2] is [00,01,11,10].
– 00 and 01 differ by one bit
– 01 and 11 differ by one bit
– 11 and 10 differ by one bit
– 10 and 00 differ by one bit
[0,2,3,1] is also a valid gray code sequence, whose binary representation is [00,10,11,01].
– 00 and 10 differ by one bit
– 10 and 11 differ by one bit
– 11 and 01 differ by one bit
– 01 and 00 differ by one bit
Example 2:

Input: n = 1
Output: [0,1]

Constraints:
1 <= n <= 16

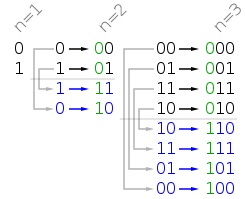
Gray Code by Recursive Mirror Algorithm

Gray code can be constructed recursively using the following Mirror method.

gray-code-mirror-algorithm

The base case when n is 1 we have [0, 1]. Then for a greater n, we reverse the result/list obtained from (n-1), and prefix it with a 1 i.e. 2^(n-1).

1
2
3
4
5
6
7
8
9
10
11
12

class Solution:
    def grayCode(self, n: int) -> List[int]:
        
        @cache
        def f(n):
            if n == 1:
                return [0, 1]
            prev = f(n - 1)
            k = 1 << (n - 1)
            return prev + [k + x for x in prev[::-1]]
        
        return f(n)

class Solution:
    def grayCode(self, n: int) -> List[int]:
        
        @cache
        def f(n):
            if n == 1:
                return [0, 1]
            prev = f(n - 1)
            k = 1 << (n - 1)
            return prev + [k + x for x in prev[::-1]]
        
        return f(n)

The time/space complexity is O(2^n)

–EOF (The Ultimate Computing & Technology Blog) —