Teaching Kids Programming – Introduction to Prim’s Minimum Spanning Tree (Graph Algorithm)

Teaching Kids Programming: Videos on Data Structures and Algorithms

Introduction to Minimum Spanning Tree MST

Previously, we have talked about the Kruskal’s MST Algorithm: Teaching Kids Programming – Introduction to Kruskal’s Minimum Spanning Tree (Graph Algorithm).

A Minimum Spanning Tree (MST) is a Tree 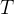that is a subset of a weighted undirectional Graph 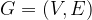aka 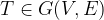. With Kruskal’s algorithm, we start with a forest will all vertice V and then add N-1 edges (N-1 edges to connect N vertex).

The total weights of the MST 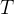is:

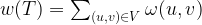
We need to pick exactly N-1 edges to build a MST with N vertices.

The Prim’s Minimum Spanning Tree (Graph Algorithm)

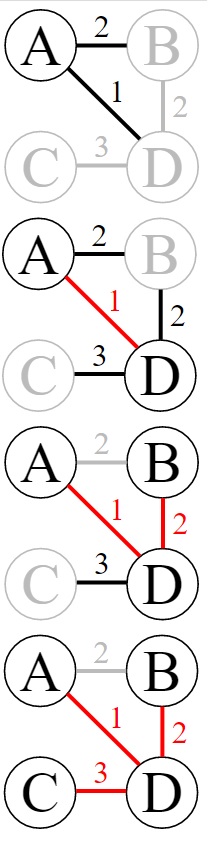
The Prim’s algorithm works differently: by adding vertices one by one in a way that every time we select the smallest edge that connects to the visited vertices.

The steps of applying the Prim’s MST Algorithm:

• 
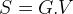
• Pick a random vertex and put it in MST T
• While T does not have N vertice yet
• – find the smallest edge (m, n) where 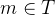and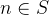
• – add the edge (m, n) to T e.g. T = T ∪ {(m, n)}
• – remove the vertex n from S

The Psuedo code:

1
2
3
4
5
6
7
8
9
10

def Prims(G):
    E = ∅;
    # pick vertex 1 (or another random)
    V = { 1 };
    while V ≠ G.V:
       # find the smallest edge such that m ∈ V and n ∈ G.V - V
       (m, n) = findEdge(V, G.V - V, G.E) 
       E = E ∪ {(m, n)}
       V = V ∪ {n}
    return {V: V, E: E}

def Prims(G):
    E = ∅;
    # pick vertex 1 (or another random)
    V = { 1 };
    while V ≠ G.V:
       # find the smallest edge such that m ∈ V and n ∈ G.V - V
       (m, n) = findEdge(V, G.V - V, G.E) 
       E = E ∪ {(m, n)}
       V = V ∪ {n}
    return {V: V, E: E}

The Prim’s Minimum Spanning Tree Algorithm can be visualized as follows – always pick the smallest edge (Greedy) that connects two vertices one from the unvisited vertices and one from the chosen set of vertices.

The time complexity is 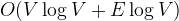which is 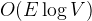. It takes 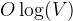to insert a vertex into a heap.

Correctness Proof of Prim’s MST Algorithm

We have chosen a list of vertex V, and by choosing a next edge we connect the current Tree (subset of MST T) to another vertex. If the next edge we pick E’ is not the smallest edge E, thus the E’ will form a cycle and can be replaced with E.

–EOF (The Ultimate Computing & Technology Blog) —