Teaching Kids Programming – Maximum Number of Space Partitions by N Straight Lines (Pizza Cutting Problem, Math, DP, Recursion)

Teaching Kids Programming: Videos on Data Structures and Algorithms

Given a Pizza or Cake or whatever circle-shape like thingy, if we can cut N times, what is the maximum number of pieces that we can get? This is equivalent to Maximum Number of Space Partitions by N Straight Lines.

Maximum Number of Space Partitions by N Straight Lines

Recursive Formula to Compute the Max Number of Partitions

The recursive formula for the maximum number of space partitions created by N straight lines can be defined as follows:

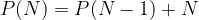
In this recursive formula, P(N) represents the maximum number of partitions created by N lines, P(N-1) represents the maximum number of partitions created by (N-1) lines, and N represents the number of the new line being introduced.

To understand the recursion, let’s consider an example. Suppose we know that the maximum number of partitions created by (N-1) lines is P(N-1). When we introduce the Nth line, it can intersect the existing (N-1) lines at most N times, creating N additional partitions. Hence, the total number of partitions created by N lines is the sum of the partitions created by (N-1) lines and the new partitions created by the Nth line.

By using this recursive formula, we can calculate the maximum number of partitions created by N straight lines by iteratively applying the formula starting from the base case:

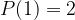or 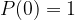zero cuts – we have only one piece.

Recursive Algorithm and Dynamic Programming Algorithm to Compute the Number of Partitions

Based on the above Recursive formula, we can implement the Top Down Dynamic Programming aka Recursion + Memoziation:

1
2
3
4
5
6

@cache
def f(n):
    if n == 0:
        return 1
    assert n > 0
    return f(n - 1) + n

@cache
def f(n):
    if n == 0:
        return 1
    assert n > 0
    return f(n - 1) + n

Or, we can do this bottom up manner – Bottom Up Dynamic Programming:

1
2
3
4
5
6
7
8
9
10

@cache
def f(n):
    if n == 0:
        return 1
    assert n > 0
    prev = 0
    ans = 1
    for i in range(1, n + 1):
        prev, ans = ans, ans + i
    return ans

@cache
def f(n):
    if n == 0:
        return 1
    assert n > 0
    prev = 0
    ans = 1
    for i in range(1, n + 1):
        prev, ans = ans, ans + i
    return ans

We add @cache to remember the f(i) value once it has been computed – since the value won’t change and can be cached if later being needed again. However, the time complexity won’t benefit much from caching the f values since each f(i) is computed once. Both approaches have O(N) time. The bottom up Dynamic Programming Algorithm has O(1) space while the Recursive version (Top Down Dynamic Programming via Memoziation) has O(N) space.

Math Equation to Compute the Max Number of Partitions

If we plot the N and F(N) on a X-Y axis, we can see it is a parabola equation, thus:

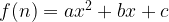
And if we plug in f(0), f(1), and f(2) or any different three random points, we can solve the quadratic equation that contains unknown a, b and c.

a=0.5, b=0.5 and c=1.

Thus: The maximum number of space partitions created by N straight lines is given by the formula:

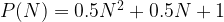
Here, P(N) represents the maximum number of partitions created by N lines.

To understand this formula, let’s consider the number of partitions created by each additional line. When we introduce the first line, it divides the space into two regions. The second line can intersect the first line at most once, creating two additional regions. The third line can intersect the first two lines at most twice, creating three additional regions. As we continue adding lines, each new line can intersect the existing lines at most N times, creating N+1 additional regions.

Hence, the number of partitions created by N lines is the sum of the number of regions created by each line:

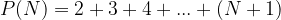
Using the formula for the sum of an arithmetic series, we can simplify this expression:

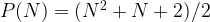
Therefore, this formula gives us the maximum number of partitions created by N straight lines in space.

Since, we have this equation, we can implement it straight away in Python via O(1) constant time/space complexity:

1
2
3

@cache
def f(n):
    return int(0.5*n*n + 0.5*n + 1)

@cache
def f(n):
    return int(0.5*n*n + 0.5*n + 1)

We can also use math.pow(n, 2) or n**2 to compute the n to the power of two.

–EOF (The Ultimate Computing & Technology Blog) —