Teaching Kids Programming – MinMax Algorithm in Game Tree (Game Theory, Tic Tac Toe)

Teaching Kids Programming: Videos on Data Structures and Algorithms

The total number of possible game states in a Tic-Tac-Toe is 3^9 which is 19683, so small that we can bruteforce using computer.

Decision Tree in Game Playing

As the number of moves can be up to at most 9, we can apply a decision tree when choosing a next move. For example, the rules could be sorted in order of priority, we just need to check if condition has been met for each rule, if yes, choose it, otherwise move to next move. If all rules are exhausted, we can switch to a random move (stochastic game policy)

Example game rules for a Tic-Tac-Toe Game:

1. Pick a slot that will checkmate
2. Pick a slot that will block opponent’s (the other player) checkmate.
3. If a central slot is available, pick it
4. If a corner slot is available, pick it

For a game with a much bigger search space such as chess, the a solo decision tree may not be enough. We can however apply decision tree for some special cases after more intelligent algorithms such as alpha-beta pruning is applied.

Minmax Algorithm in Two Player Zero Sum Game Tree

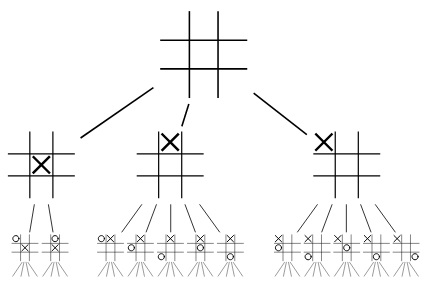
The Tic-Tac-Toe game can be visualized as the following:

Tic Tac Toe Game Tree

Two players take turn: the agent tries to maximize the score, and the opponent tries to do the opposite aka minimize the score.

The following is a Python function (Recursive) to apply the MinMax Algorithm in a Game Tree. We pass down the depth, turn (used to indicate are we maximizing or minimizing in this turn), and a game state. We can however, split the minmax function into two: min, and max where the min calls max, and max calls min.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

def minmax(self, depth, turn, state):
    if self.isEnd(state):
        return self.utility(state)
 
    bestAction = None
    actions = self.actions(state)
    if turn:
        score = -math.inf
        for action in actions:
            newState = self.succ(state, action)
            _, curScore = self.minmax(depth + 1, -turn, newState)
            if curScore > score:
                score = curScore
                bestAction = action
        return bestAction, score
    else:
        score = math.inf
        for action in actions:
            newState = self.succ(state, action)
            _, curScore = self.minmax(depth + 1, -turn, newState)
            if curScore < score:
                score = curScore
                bestAction = action
        return bestAction, score

def minmax(self, depth, turn, state):
	if self.isEnd(state):
		return self.utility(state)

	bestAction = None
	actions = self.actions(state)
	if turn:
		score = -math.inf
		for action in actions:
			newState = self.succ(state, action)
			_, curScore = self.minmax(depth + 1, -turn, newState)
			if curScore > score:
				score = curScore
				bestAction = action
		return bestAction, score
	else:
		score = math.inf
		for action in actions:
			newState = self.succ(state, action)
			_, curScore = self.minmax(depth + 1, -turn, newState)
			if curScore < score:
				score = curScore
				bestAction = action
		return bestAction, score

Game Theory – Game Algorithms

• Teaching Kids Programming – Alpha Beta Pruning Algorithm on NegaMax (Game Theory)
• Teaching Kids Programming – NegaMax Algorithm (Game Theory)
• Teaching Kids Programming – Alpha-Beta Pruning Algorithm (Game Theory)
• Teaching Kids Programming – Define Tic Tac Toe using Game Theory Terminologies
• Teaching Kids Programming – Introduction to Two Players Zero-Sum Game (Number Halving)
• Teaching Kids Programming – MinMax Algorithm in Game Tree (Game Theory, Tic Tac Toe)

–EOF (The Ultimate Computing & Technology Blog) —