Teaching Kids Programming – Probability Matrix of Walking in a Grid (Unique Paths)

Teaching Kids Programming: Videos on Data Structures and Algorithms

On a grid that each step, we can only walk east and south (each 50%), we want to find out the probability of reaching a position. This is similar to Day 99 where we talked about the number of unique paths using Dynamic Programming or Math Combination. We can compute the probability from the top left corner (start) – which is 100%, and if there are two next moves, we can then split into two with x50%, otherwise we following along the way. And for each new position, the probability is accumulated from possible two sources (r-1,c) or (r, c-1).

The Probability Matrix looks like this for a 3×3 grid:

1,    1/2,  1/4
1/2,  1/2,  1/2
1/4,  1/2,  1

The bottom-right corner should be 100% as all paths lead to it. The Probability Matrix is also symmetric.

If the east and south directions are 50/50, we can also compute the probability via t/T where t is the number of paths passing through, and T is the total number of paths (passing through plus passing by).

Recall that, the below matrix shows the number of paths passing through each cell: [maht] F(r, c) = F(r – 1, c) + F(r, c – 1) [/math] where 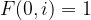and .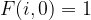

1 1 1
1 2 3
1 3 6

For example, the probability of the cell (with number 6) can be computed via the paths going through 6 and passing by which are 3+3 and 0, thus the probability is 6/(6+0)=100%

For cell (with number 2), the probability can be calculated via the paths going through 2 and passing by which are 2 and (1+1), thus the probability is 2/(2+1+1)=50%.

Algorithms to Walk in a Grid

Here are some posts on the path counting or probability on a Grid:

• Teaching Kids Programming – Probability Matrix of Walking in a Grid (Unique Paths)
• Teaching Kids Programming – Count Number of Ways to Walk in a Grid using Dynamic Programming or Combination
• How Many Ways from A to C via B?

–EOF (The Ultimate Computing & Technology Blog) —